首先,更正上篇文章的单位mΩ不正确,应该为μΩ,本篇有接触电阻举例计算,请以本篇为准。
一、螺栓选型
1、螺栓选型
铜母排连接中常使用镀锌钢螺栓,但更推荐使用铜合金螺栓(如铝青铜 CW307G)。因为铜合金螺栓的热膨胀系数与铜的热膨胀系数更为接近,有助于维持接触压力的稳定;
此外,铜合金螺栓还能避免异种金属腐蚀问题,在存在强磁场的环境中也更具优势。
不过,由于这些铜合金材料的屈服应力不明显,在紧固过程中需特别注意,避免超过规定的紧固扭矩;
同时,在整个工作温度范围内,螺栓所承受的应力不应超过其弹性极限的 95%。
铜与几种典型螺栓材料的弹性极限和热膨胀系数对比详见下表,从表中数据可以清晰地看出,螺栓材料的选择对连接的热稳定性具有决定性影响。
铜与典型螺栓材料的弹性极限及热膨胀系数对比
| 材料 | 弹性极限(MPa) | 热膨胀系数(每℃) |
| 铜 | 完全退火态:50;
全硬化态:340 |
16.5×10⁻⁶ |
| 高强度钢 | 700 | 11.1×10⁻⁶ |
| 316 不锈钢 | 414 | 15.9×10⁻⁶ |
| 铝青铜
(CW307G) |
400 | 16.2×10⁻⁶ |
| 304 不锈钢 | 207 | 17.2×10⁻⁶ |
| 硅青铜
(C651000) |
365 | 17.8×10⁻⁶ |
2、温度影响
温度升高(Δ T)引起的拉力增量(F_supp)可通过以下公式计算:
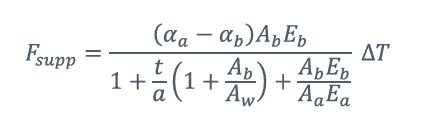
式中:
α_a—— 母排导体的热膨胀系数;
α_b—— 螺栓的热膨胀系数;
A_b—— 螺栓的横截面积;
E_b—— 螺栓的弹性模量;
E_a—— 母排的弹性模量;
t—— 垫圈的厚度;
a—— 母排的厚度;
A_w—— 垫圈下方的表观面积;
A_a—— 接头重叠区域的表观面积。
螺栓应力的变化量与热膨胀系数差值(α_a -α_b)成正比。
例如,若采用高强度钢螺栓连接,由于热膨胀系数差值较大(Δα = 5.5×10⁻⁶/℃),螺栓的拉力会显著增大;
而若采用 CW307G 铝青铜螺栓,热膨胀系数差值很小(Δα=-0.3×10⁻⁶/℃),螺栓拉力仅会轻微减小。
3、螺栓应力
无论采用何种螺栓材料,在设计接头时都必须确保:在整个工作温度范围内的任何温度下,螺栓所承受的最大拉力都应小于其屈服强度的 95%。若超过这一限值,螺栓可能会发生塑性变形,最终导致接头松动失效。
计算螺栓应力时,应采用螺栓的抗拉应力面积(具体数值可参考表 1),而非螺栓的公称面积。
表 1 典型螺纹特性参数

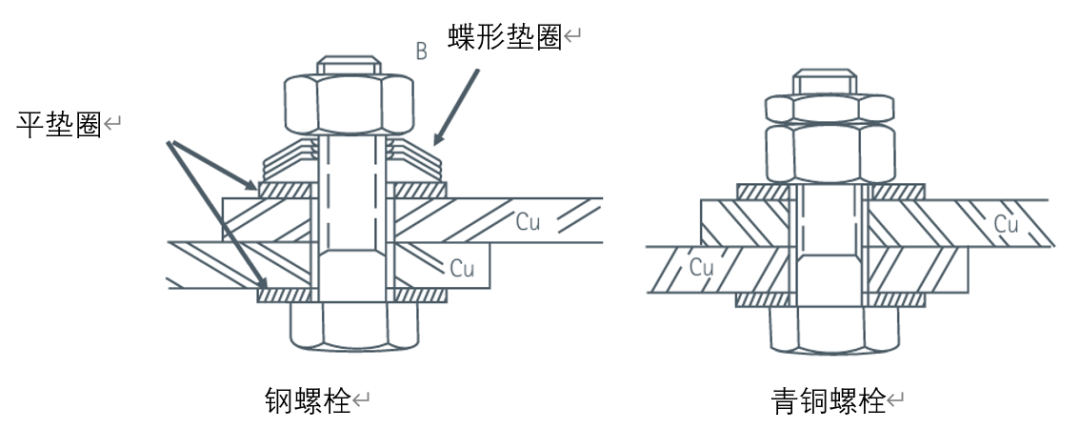
若设计要求必须使用高强度钢螺栓,此时拉力增量F_supp可能会超过螺栓弹性极限的 95%。在这种情况下,需使用碟形弹簧垫圈(也称为贝勒维尔垫圈),如图所示。
选择合适高度和弹簧刚度的垫圈,可通过以下公式降低F_supp的值:
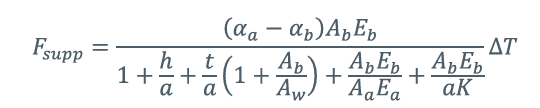
式中:
h—— 碟形弹簧垫圈的总高度;
K—— 碟形弹簧垫圈的弹簧刚度。
在实际组装过程中,首先按照规定的扭矩紧固螺栓,以确保获得所需的接触压力;在接头投入使用后,当温度升高时,碟形弹簧会被压缩,从而将螺栓拉力的增量限制在安全范围内。
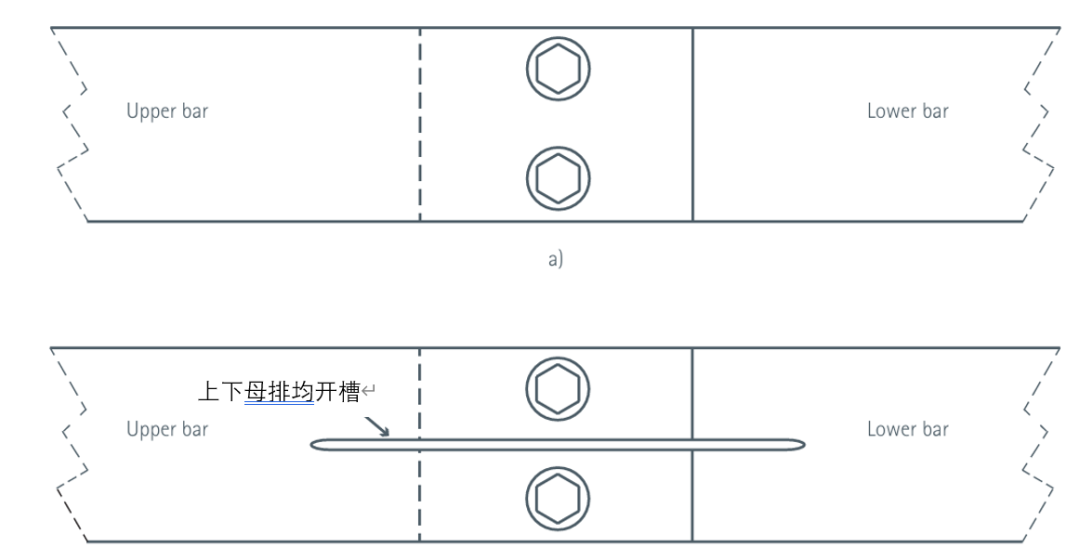
4、开槽优化
此外,通过改变螺栓连接的设计(例如在母排上开设纵向槽,如图所示),可使接触电阻降低 30%-40%。
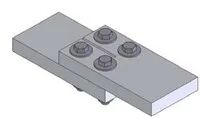
电阻降低的原因是,这种设计能改善接头每个分支处的接触压力均匀性,进而增大接触面积。
二、螺栓布置方式
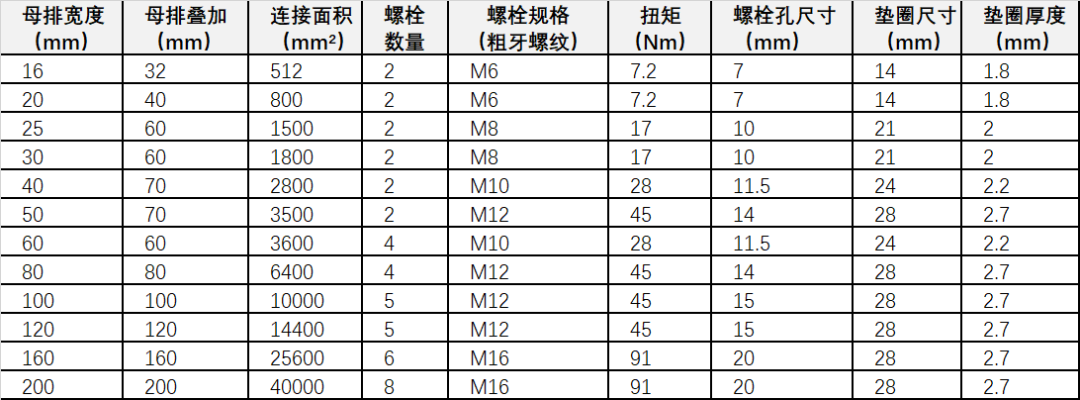
尽管针对具体的安装场景,螺栓的布置方式应通过计算确定,但许多资料中都提供了相关的推荐方案。下表中列出的螺栓布置方案已应用多年,可作为初步设计时的参考依据。
表中推荐的扭矩值适用于高强度钢(8.8 级)或铝青铜(CW307G,旧型号为 C104)紧固件,且这些紧固件的螺纹为标准粗牙螺纹,表面粗糙度为常规水平,未进行额外润滑处理。
表2典型的铜母排螺栓布置方案(单面重叠连接)
三、连接效率
连接效率:通常用包含接头的导体段电阻与相同长度的直导体电阻比值来衡量。
通过优化设计,可以实现连接效率值低于 100% 的接头,即接头的电阻低于相同长度直导体的电阻。
在整个母排系统中,由于受接头影响的部分所占比例相对较小,因而接头效率对系统整体性能的影响有限。
但接头效率仍在以下两个方面具有重要意义:
1、效率高于 100% 的接头,由于电阻较高,其工作温度会高于正常母排的温度,并且温度波动幅度较大,长期会影响接头的使用寿命。
2、在开关柜等设备中,通常会密集布置多个接头。效率较低的接头会导致设备内部产生过多热量,温升会造成更大的电压降。
四、连接效率计算
1、公式推导
如前所述,接头的电阻由两部分组成:一部分是电流流动轨迹扭曲产生的电阻(即流线效应电阻),另一部分是接触电阻。
对于重叠连接,由流线效应产生的电阻可通过以下公式计算:
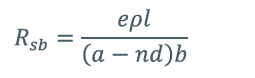
式中:
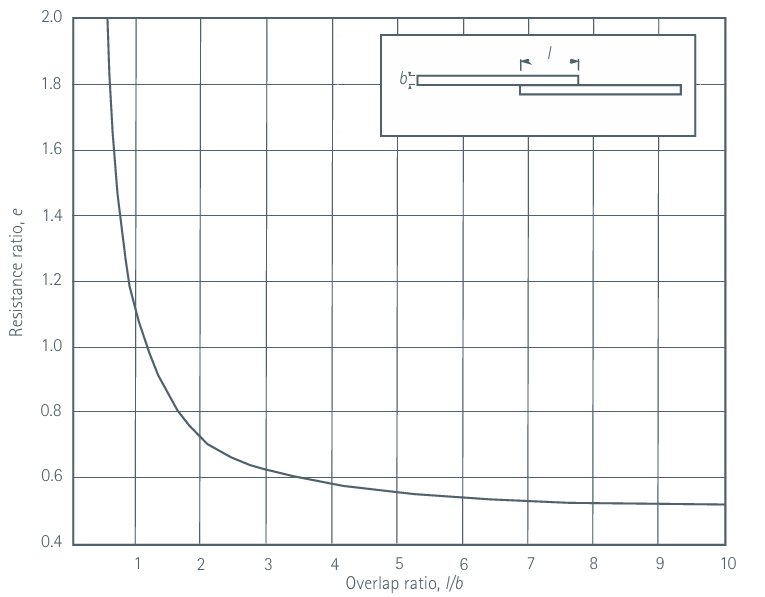
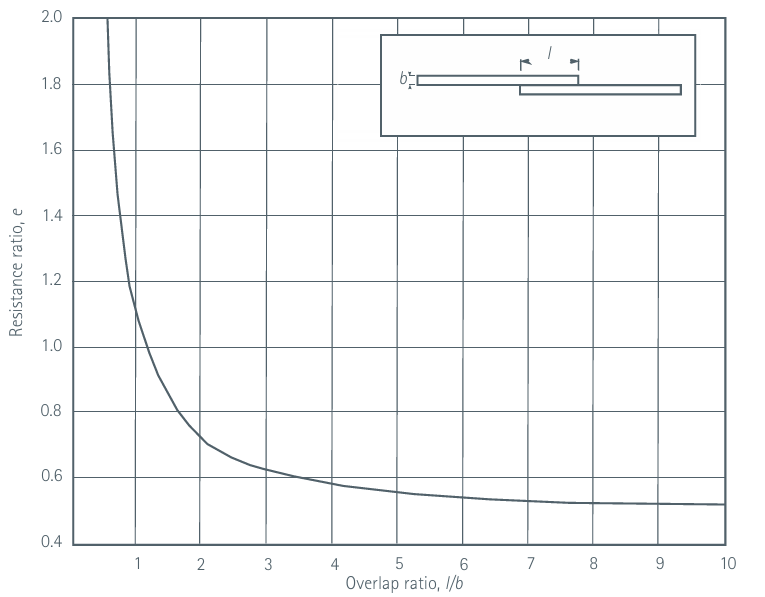
e—— 电阻比,可从图1中获取;
a—— 母排宽度(单位:mm);
b—— 母排厚度(单位:mm);
l—— 重叠长度(单位:mm);
ρ—— 导体的电阻率(单位:μΩ・mm,对于 100% IACS(国际退火铜标准)的铜,电阻率取值为 17.24μΩ・mm);
d—— 螺栓孔的直径(单位:mm);
n—— 母排宽度方向上螺栓孔的数量(对于夹紧连接,n = 0)。
接头的接触电阻R_i可通过以下公式计算:
R_i = Y / al
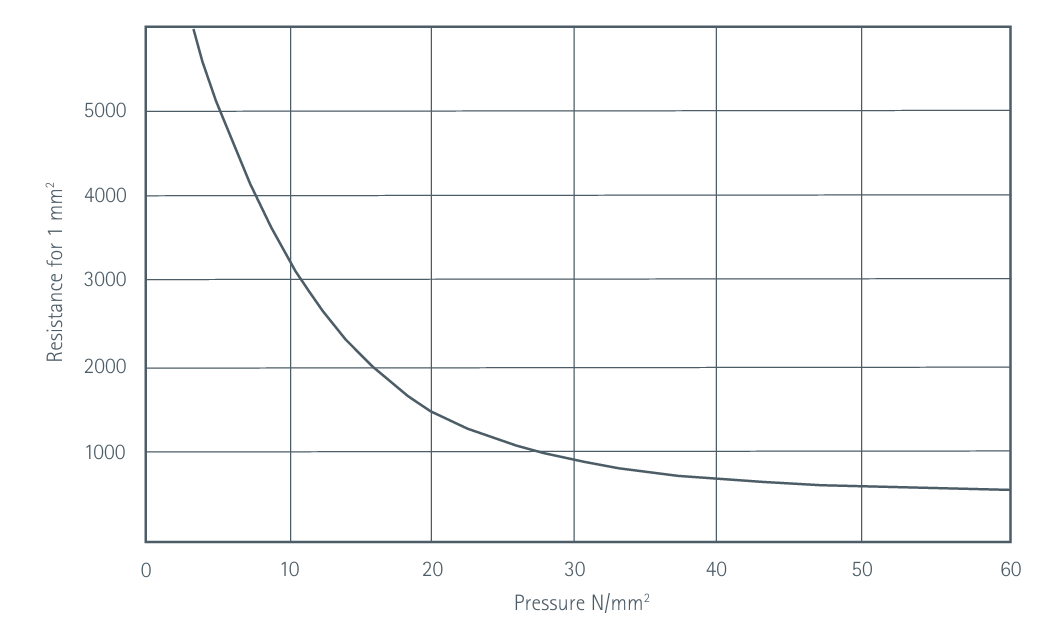
式中,Y为单位面积的接触电阻,可从图2中获取。
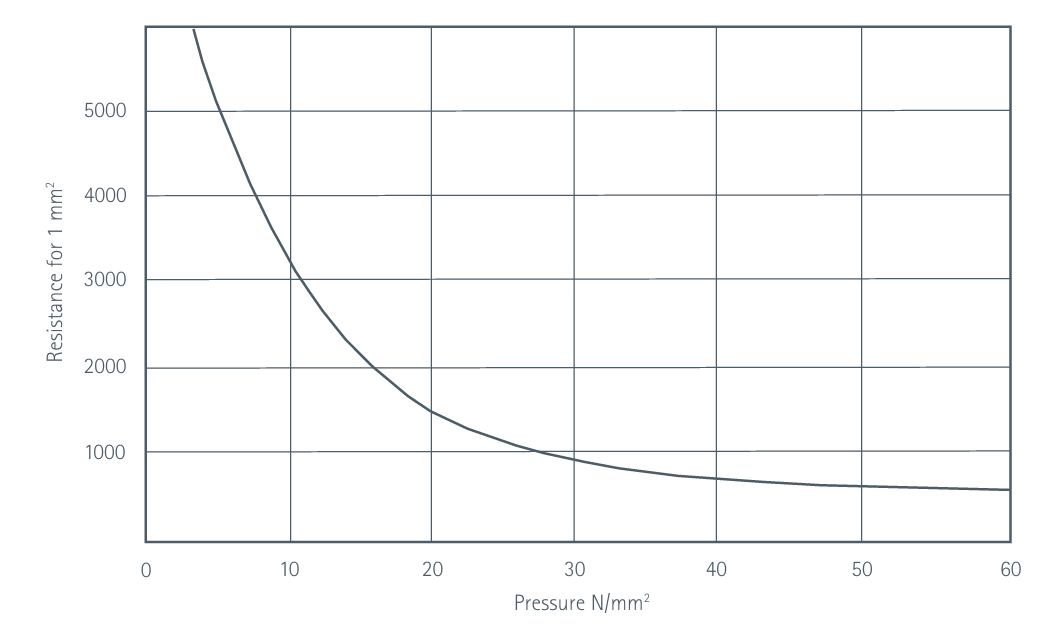
图2注:纵轴为 1mm² 面积的电阻值(单位:μΩ),范围 0-5000μΩ;
横轴为压力(单位:N/mm²),范围 0-60N/mm²。
因此,接头的总电阻R_j为:
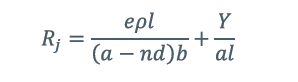
由于相同长度直导体的电阻R_b为:
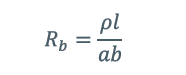
则接头的连接效率可表示为:
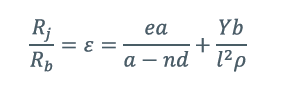
从上述公式可以看出,影响接头效率的关键因素,是螺栓孔导致的母排横截面积减小,即公式中的nd项。
2、举例计算
以表 2中叠加长度为 70mm、规格为 50mm×10mm 的铜母排为例,计算其接触力F(已知采用 2 个 M12 螺栓):
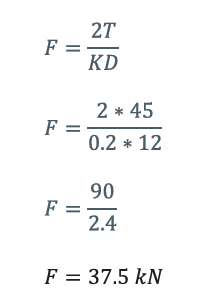
接头的接触面积为 3500mm²,因此接触压力P为:
P= F / 3500
P = 10.7 N/mm²
从图中可查得,对应的Y值为 3000μΩ・mm²。
对于厚度为 10mm 的母排,重叠长度与厚度的比值为 7,从图中可查得电阻比e = 0.55。
将上述参数代入效率计算公式:
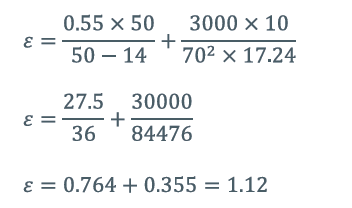
由此可知,该接头的电阻是长度为 70mm、规格为 50mm×10mm 的铜母排电阻的 1.12 倍,等效于长度为 78.4mm 的该规格铜母排的电阻。因此,该接头的温度会略高于周围母排的温度。
若对该接头进行重新设计,将重叠长度增至 90mm,并采用 3 个同规格螺栓(保持扭矩不变),则接头效率会发生如下变化:
此时螺栓的总拉力F = 56.25kN;
接头面积变为 4500mm²,接触压力P为:
P= F /4500
P = 12.5 N/ mm²
从图中可查得,对应的Y值为 2600μΩ・mm²;
对于厚度为 10mm 的母排,重叠长度与厚度的比值变为 9,从图中可查得电阻比e = 0.52;
将这些参数代入效率计算公式:

在这种情况下,该重叠长度90mm铜排接头的电阻为铜母排电阻的 0.91 倍,等效于长度为 82mm 的该规格铜母排的电阻。
上面的推导只是一个粗略的计算过程,实际还要考虑螺栓开通的影响。
本文主要内容来自:铜业协会的铜母排设计与安装指南中David Chapman编写的铜母排连接
本篇文章来源于: 新能源安全技术

