摘要:降低模块化多电平变换器(modular multilevel converter, MMC)子模块电容电压波动对提高MMC功率密度,实现MMC轻型化具有重要意义。在降低MMC子模块电容电压波动的方案中,飞跨电容MMC(flying-capacitorMMC, FC-MMC)以其良好的性能得到了广泛的关注。基于传统FC-MMC方案,提出了一种采用Si IGBT与SiC MOSFET混合器件的FC-MMC拓扑,该拓扑每个桥臂包括两个SiC子模块及多个Si子模块,减少了SiC功率器件的使用量。进而提出了相应的调制策略,将大部分开关动作转移到SiC子模块,充分利用了SiC MOSFET开关损耗低和Si IGBT导通损耗低的优势,在不过多增加成本的情况下,降低了FC-MMC的总损耗。通过实验和损耗分析验证了所提方案的有效性和可行性。
关键词:FC-MMC;混合器件拓扑;改进调制策略;SiC MOSFET;Si IGBT;损耗优化
0.引言
模块化多电平变换器(modular multilevel converter,MMC)由于具有模块化程度高、可扩展性强、波形质量好、谐波含量低等优点,在直流传输、电机驱动、可再生能源集成等领域有着广阔的应用前景。电容作为MMC的核心储能元件,其体积和质量占子模块的一半以上,成本约占变换器总成本的1/3,因此其容值优化问题受到广泛关注。其中,电容电压波动是影响子模块电容容值的主要因素。目前降低MMC子模块电容电压波动的方案主要分为两类:附加控制类和拓扑改进类。
附加控制类方案主要包括二倍频环流分量注入、高频共模电压分量注入和三次谐波电压分量注入3种。高频注入法虽然能在一定程度上降低子模块电容电压波动,但增加了器件电流应力和变换器功率损耗。拓扑改进类方案主要包括子模块拓扑和功率通道拓扑两种。文献[12]在每个子模块上并联一个有源电力滤波器(active power filter,APF)电路,使用辅助电容来吸收纹波电压。然而,新的子模块拓扑需要两倍数量的功率器件和电容。文献[13]基于上下桥臂脉动功率基频分量反相的原理,在子模块之间构建隔离型双向变换器作为功率通道,使得脉动功率相互流通抵消,进而降低低频电压脉动。同样,这种方案需要两倍数量的功率器件且控制复杂。
文献[14]提出了一种飞跨电容型模块化多电平变换器(flying-capacitor MMC,FC-MMC),该拓扑利用一个电容连接每相上下桥臂中点,用来传输高频脉动功率。通过控制飞跨电容电流,可以实现桥臂之间的功率平衡,从而大幅降低子模块电容电压波动。该方案不增加功率器件的数量,且没有共模电压流向交流侧。传统FC-MMC采用载波移相调制,为实现桥臂间功率平衡,保证高频电流电压波形质量,需要较高开关频率。同时开关频率的提升可以降低对飞跨电容容值的需求,因此具有更低开关损耗的宽禁带半导体器件在FC-MMC中有良好的应用前景。
然而宽禁带器件高昂的成本限制了其应用,目前主流方案是采用SiC MOSFET与Si IGBT混合器件拓扑,以实现损耗和成本的优化。文献[16]分析了不同器件组合下半桥子模块损耗,并提出一种SiIGBT与SiC MOSFET混合器件并联子模块拓扑,每个功率管流经电流为传统拓扑一半,在相同损耗下实现了开关频率的提升。文献[17]提出一种采用混合器件的电容开关型全桥子模块拓扑(capacitorswitching-full bridge submodule,CS-FB SM),文献[18]在此基础上提出一种电容开关型半全桥子模块拓扑,这两种方案利用器件均流现象和SiC Diode的快恢复特性,降低了变换器损耗。然而上述方案每个子模块均需要添加一个SiC MOSFET开关管,成本优化有限。文献[19]提出了一种混合型MMC拓扑及调制策略,充分利用了SiC MOSFET低开关损耗和Si IGBT低导通损耗的优势,且每个桥臂仅包括一个SiC全桥子模块,实现了损耗和成本的优化。该方案在FC-MMC中的应用存在改进的空间。
本文主要内容如下:首先介绍了FC-MMC的拓扑结构,分析了FC-MMC的工作原理,推导了桥臂功率平衡表达式。接着,从功率脉动的角度建立了传统MMC的数学模型,推导了子模块电容电压波动表达式,并介绍了电容开关型全桥子模块拓扑,分析了该拓扑的损耗特性。基于上述分析,提出了一种Si IGBT与SiC MOSFET混合的FC-MMC拓扑及其调制策略。在新调制策略下,开关动作大部分集中在SiC MOSFET上,充分利用了SiC MOSFET低开关损耗和Si IGBT低导通损耗的优势,降低了FC-MMC总损耗。最后通过实验和损耗分析验证了所提方案的有效性和可行性。
1. FC-MMC拓扑结构与工作原理
1.1 FC-MMC拓扑结构
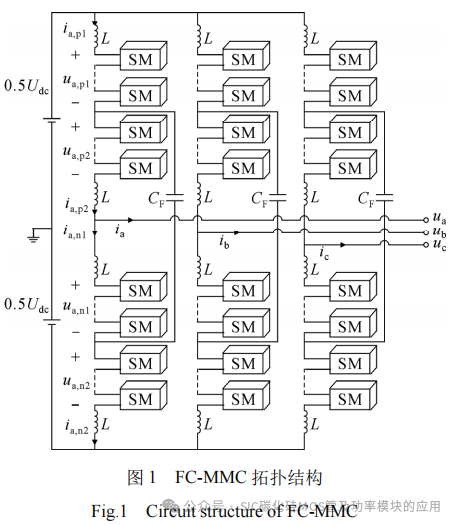
FC-MMC拓扑结构如图1所示。每个相单元包括上桥臂、下桥臂和飞跨电容3部分,通过飞跨电容CF连接上下桥臂中点,进一步将桥臂分为上半桥臂与下半桥臂。ux、ix为输出相电压和相电流,其中x(=a,b,c)代表三相单元;半桥臂电压分别表示为ux,p1、ux,p2、ux,n1、ux,n2;半桥臂电流分别表示为ix,p1、ix,p2、ix,n1、ix,n2;Udc为直流母线电压。每个半桥臂包括N/2(N取偶数)个子模块和一个桥臂电感L,桥臂两端由缓冲电感连接到直流侧和交流输出侧,以减小桥臂电流波动。
1.2 FC-MMC工作原理
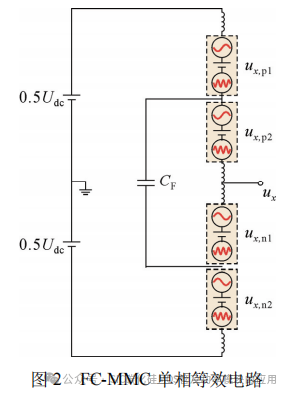
为简化FC-MMC工作原理的描述,将其拓扑转换为单相等效电路,如图2所示,级联子模块用受控电压源替代。FC-MMC每相4个半桥臂单独调制,桥臂电压包括3部分:直流分量Udc、基频分量ux和高频分量uh,x,其表达式为
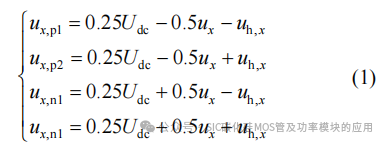
式中:上下桥臂基频分量ux反向以支撑交流侧输出电压,直流分量Udc同向以支撑直流母线电压。在每个半桥臂中注入幅值相同、相位相反的高频电压分量uh,x,桥臂总电压维持不变。注入的高频电压分量由于相位相反,对直流和交流侧的影响相互抵消,不会影响直流侧电压和负载侧的共模电压。
控制流经飞跨电容的电流ih,x与uh,x同频率同相位,则上、下半桥臂电流为
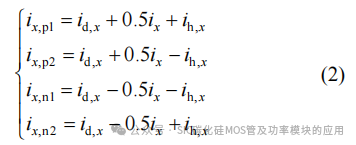
式中:id,x为直流母线电流;ix,p1、ix,p2分别为上、下半桥臂电流。基频分量和高频分量如式(3)所示。

式中:Um、Im分别为输出电压、输出电流幅值;Uhm和Ihm分别为高频电压分量uh,x和高频电流分量ih,x的幅值;θx和φ是输出电压和输出电流的相位角;ωh=2πfh为注入高频分量角频率。
尽可能提高注入高频电压的幅值,使其达到
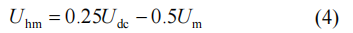
在正常工况下调制比足够大,高频电压分量占比较小,此时上半桥臂与下半桥臂电压相近,桥臂子模块投入数在上下半桥臂均分,飞跨电容承受的电压应力为Udc/2,均匀分布在两个半桥臂(ux,p2与ux,n1)投入的子模块以及两个桥臂电感上。
桥臂电流与桥臂电压各分量相乘即得到FC-MMC上、下桥臂功率px,p、px,n表达式为
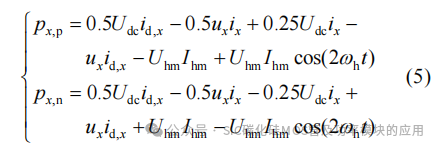
式中,前4项为直流分量与基频分量之间的相互作用,对桥臂功率波动影响较大。上下桥臂注入的高频电压和高频电流所产生的功率始终互补反向,因此可以通过飞跨电容在上下桥臂之间重新分配能量。当上桥臂功率大于下桥臂功率时,高频电流流经飞跨电容,并与下桥臂电压相互作用,从而实现了功率从上桥臂到下桥臂的转移,进而减小子模块电容电压波动。
根据桥臂功率表达式,通过控制直流电流id,x与飞跨电容电流ih,x,使脉动功率主要成分相互抵消,从而降低子模块电容电压波动,功率平衡表达式为
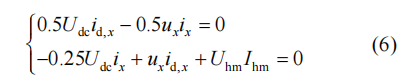
则直流分量id,x与高频分量幅值Ihm表达式为
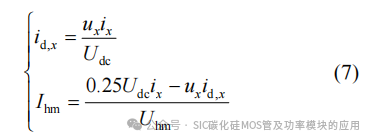
式中:id,x用于直流侧和交流侧的功率传递;ih,x的幅值Ihm按式(7)进行调制,其符号分别对应高频电压和电流同相或反相。
2.传统MMC与混合器件型子模块拓扑
2.1 MMC数学模型
传统MMC每个桥臂包括N个子模块,上下桥臂之间由桥臂电感L0连接。由于MMC三相严格对称且工作原理相同,本节以单相拓扑为例,从功率脉动的角度推导了子模块电容电压波动模型,并进一步推导了理想状态下FC-MMC的电容电压波动表达式。当确定了桥臂功率和子模块数目时,就确定了分散到单个子模块电容上的功率,桥臂脉动功率可以看作是电容储能变化的总和。
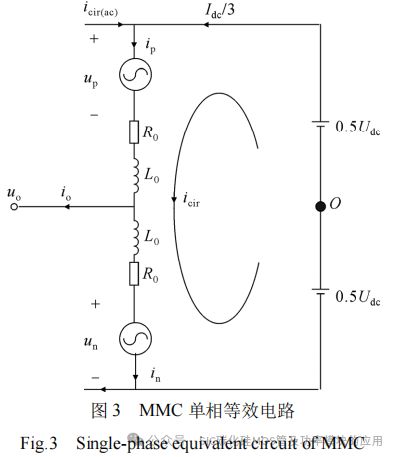
MMC单相等效电路如图3所示,其中icir为桥臂环流,Idc为直流电流,up、un为上、下桥臂电压。上下桥臂中串联的子模块等效为受控电压源,R0为桥臂等效电阻。基于该等效电路,根据基尔霍夫电流定律,上下桥臂电流表达式为

式中:ip、in为上、下桥臂电流;io为交流侧输出电流;icir为相间环流,主要包括直流成分和偶次谐波成分。直流成分可以看作直流电流在三相单元中的均分,偶次谐波成分则以二次环流分量为主。
基于基尔霍夫电压定律,桥臂电压表达式为
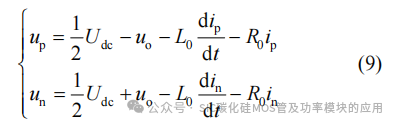
式中:uo为交流侧输出电压;up、un为上、下桥臂电压,交流侧输出电压和电流可表示为
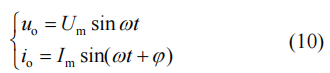
在不考虑换流器损耗和功率器件损耗的情况下,系统一个周期内交流侧和直流侧的有功功率均值Pdc、Pac相等,可表示为
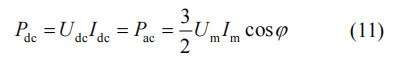
根据式(11),直流侧电流Idc可以表示为
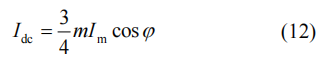
式中,m=2Um/Udc,为输出电压调制比。将式(12)和式(10)代入式(8),忽略环流中的高频成分,得到桥臂电流表达式,如式(13)所示。其中I2f为二倍频环流幅值,φf为其初相角。

忽略桥臂电感和桥臂等效电阻上的压降,则桥臂电压可以表示为
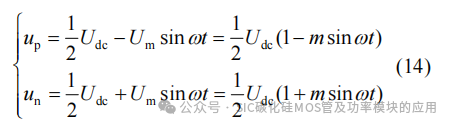
由此,上下桥臂电压和电流表达式都已得到,则上、下桥臂功率pp(t)、pn(t)即为电压电流的乘积,可以表示为

子模块电容的瞬时脉动功率ΔE表达式为
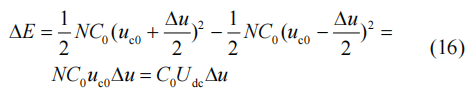
式中:uc0是子模块平均电容电压,其大小等于Udc/N;Δu为电容脉动电压。对式(15)进行积分,令其等于式(16),可计算出电容脉动电压为
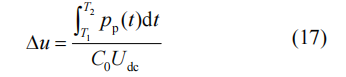
取一个周期内脉动功率的最大值,即得到子模块脉动电压的峰峰值Δup-p。
由式(5)、(6)FC-MMC功率平衡表达式可知,利用高频分量ih,x与uh,x实现功率在上下桥臂间的传递,理想状态下脉动功率完全抵消,仅剩高频交流分量,代入式(17)得到其电容电压波动表达式为
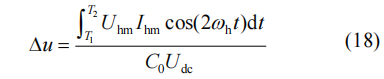
2.2 电容开关型全桥子模块拓扑
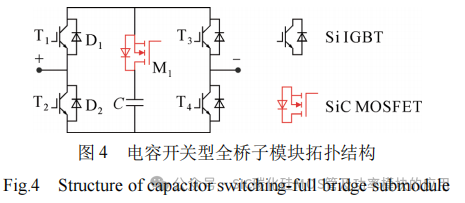
电容开关型全桥子模块拓扑如图4所示,该拓扑基于全桥结构,在电容支路串联一个SiC MOSFET开关管M1,其余开关管T1—T4采用Si IGBT。该拓扑具有正投入、负投入和切除3种工作状态。利用SiC Diode的快恢复特性和子模块输出零电平状态时的器件均流现象,降低了CS-FBMMC的损耗。其投切状态如图5所示,处于阻断状态的开关管用虚线表示,处于导通状态的开关管用实线表示。
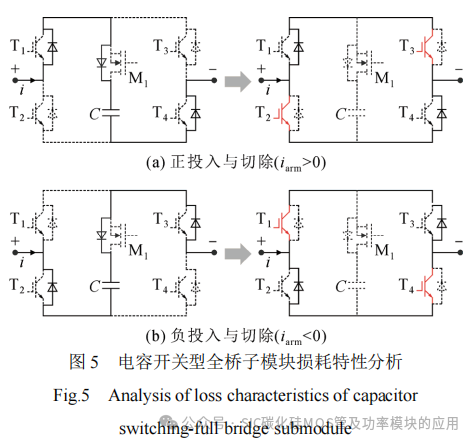
两个开关管均分电流的现象称为均流现象,根据器件手册拟合的损耗模型可知,具有均流现象的两个开关器件的损耗之和低于单个开关管的损耗。由于均流现象,使得两个开关管导通损耗之和相比于单管的损耗降低了大约20%~30%。从开关管的数学模型方面也可以得到相应的解释。均流现象引起的两个开关管的损耗相比于单管损耗,恒定电压降部分损耗相同,电阻部分减半,其损耗更低。因此,在切除状态下电容开关型全桥子模块拓扑的均流现象使其具有低导通损耗特性。
当桥臂电流为正,子模块由正投入转为切除的过程中,首先由于SiC Diode的快恢复特性,开关管M1快速关断。然后,开关管M1承受子模块电容电压,开关管T2和T3漏源极电压极低。最后,开关管T2和T3开通,由于开关管T2和T3漏源极电压极低,损耗极低,可忽略不计,其过程可以近似为零电压开通。同理,当桥臂电流为负,投切状态由负投入转为切除的过程中,开关管T1和T4快速开通,其开关损耗也极低。因此,电容开关型全桥子模块在正投入(桥臂电流>0)和负投入(桥臂电流<0)转换为切除的过程中,SiC Diode的快恢复特性使其具有低开关损耗特性。
然而,基于该拓扑的MMC每个子模块均需要一个SiC MOSFET开关管,且仅在正投入(桥臂电流>0)和负投入(桥臂电流<0)转换为切除的工况下可以利用SiC Diode快恢复特性实现开关损耗的降低,成本和损耗优化有限。
3. FC-MMC改进拓扑与调制策略
3.1改进FC-MMC拓扑
基于FC-MMC工作原理的分析可知,半桥臂电压主要包括直流成分、基频成分和高频成分,为提高半桥臂电压中高频成分波形质量,各子模块开关频率需维持在较高水平,同时提高开关频率可以降低对飞跨电容CF容值的需求。因此,具有低开关损耗的宽禁带半导体器件在FC-MMC中具有良好的应用前景。然而,SiC MOSFET高额的成本限制了其应用。同时在中高压场合下,其导通损耗显著高于Si IGBT,这是由于Si IGBT有两种载流子,具有更高的电导率[22]。因此完全将Si IGBT替换为SiC MOSFET不能降低变换器总损耗。
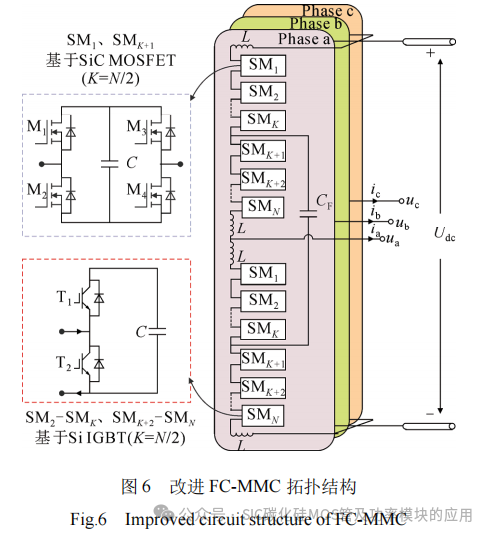
为充分利用两种功率器件的优势,改进FC-MMC拓扑结构如图6所示。与传统方案相比,其主电路结构保持不变,每个半桥臂中第一个子模块采用基于SiC MOSFET功率器件的全桥子模块,其余子模块采用基于Si IGBT功率器件的半桥子模块,即每个桥臂包括2个SiC子模块与N−2个Si子模块。与完全基于SiC MOSFET的FC-MMC相比,SiC MOSFET成本约为Si IGBT的8倍,单相4个SiC子模块显著降低了FC-MMC的成本,同时在高功率大电流场合,完全基于SiC MOSFET有更高的导通损耗;与完全基于Si IGBT的FC-MMC相比,通过新的调制策略,开关动作主要集中在SiC MOSFET,从而显著降低了变换器的开关损耗。在变换器功率>0.6 MW工况下,所提方案具有最低的总损耗。
3.2改进FC-MMC调制策略
基于第2章FC-MMC桥臂脉动功率的分析,传统FC-MMC采用载波移相调制策略(CPS-PWM),各子模块开关频率相同,根据上下桥臂功率平衡表达式计算出半桥臂各电压分量,外加对直流电流id,x与高频电流ih,x的闭环控制,以及桥臂子模块的均压控制,生成半桥臂电压调制波,与各子模块三角载波比较得到功率器件的开关信号。
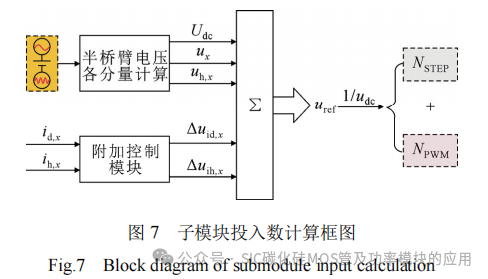
本文结合新的拓扑,提出一种新型调制策略。在生成半桥臂参考电压uref之后,将其分解为两部分,计算Si子模块投入数与SiC子模块投入数,表达式如式(19),框图如图7所示,其中Δuid,x为相单元电容电压调节分量,Δuih,x为桥臂单元电容电压调节分量。

式中:uc为子模块平均电容电压;floor为向下取整函数;NSTEP表示Si子模块投入个数,构成维持半桥臂电压的阶梯波;NPWM表示SiC子模块工作在PWM模式的占空比,以补偿正弦桥臂电压的缺失。当NPWM在0和1之间变化时,将其与三角载波比较得到SiC子模块的开关信号,使子模块正投入或切除。当流经SiC子模块的电流>0时,子模块充电;电流<0时,子模块放电。由于桥臂电流存在直流偏置,若子模块一个周期内充放电时间相同,其电压将飙升导致电容电压失衡。
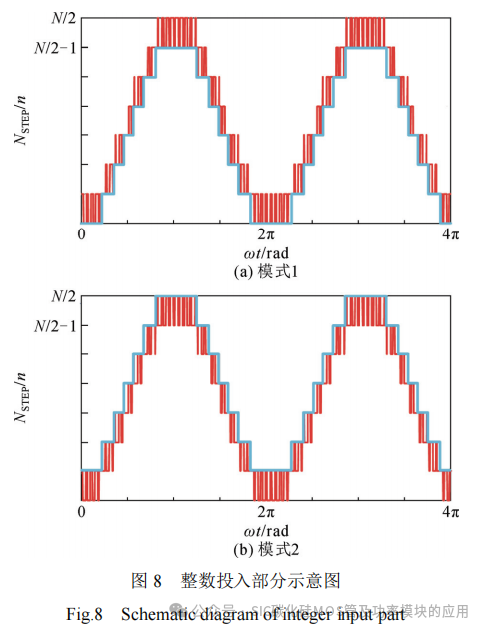
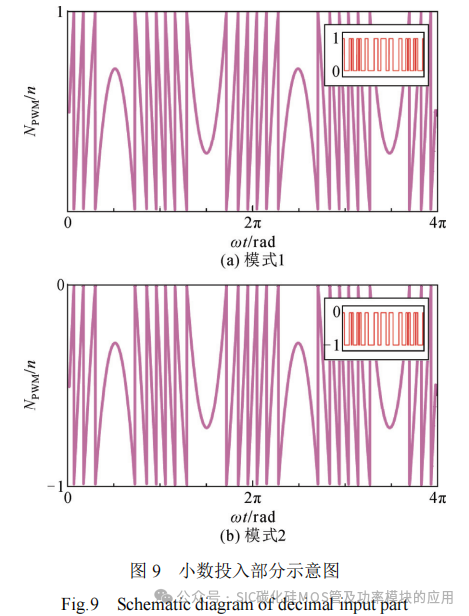
为解决此问题,可利用全桥子模块的负投入能力来增加电容放电时间。由于SiC子模块负投入时端口电压为负,需要增加Si子模块投入数来弥补半桥臂电压的损失。NSTEP与NPWM如图8和图9所示,其含义与式(19)一致。当NSTEP发生变化时,将SiC子模块电容电压与子模块平均电容电压进行比较。以电流>0为例,若SiC子模块电容电压偏低,则电容应该充电,NSTEP和NPWM不变,如式(19)所示(模式1);若其电容电压偏高,则SiC子模块进行负投入放电,同时增加Si子模块投入数以维持半桥臂电压,NSTEP和NPWM表达式如式(20)所示(模式2)
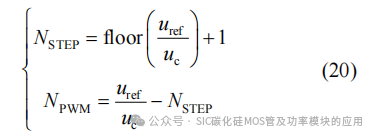
通过这种调整,桥臂电压参考值uref保持不变,NPWM在−1到0之间变化,同时三角载波反向,SiC子模块进行负投入放电。然而由于每个半桥臂中只有N/2−1个子模块工作在阶梯波模式,NSTEP不可能达到N/2,因此当阶梯数达到N/2−1时,禁止SiC子模块负投入,在此期间产生的电容电压不均可在一个周期内的其他时刻进行调整。
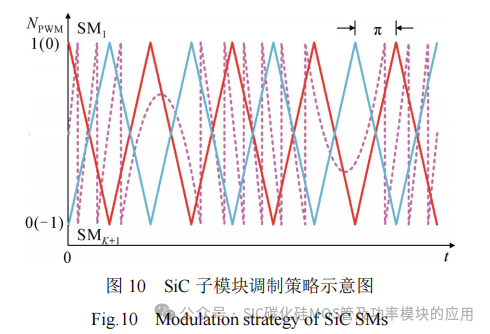
在生成调制波后,与三角载波进行比较得到SiC子模块开关信号。其中,每相桥臂的两个SiC子模块载波相差相位π,如图10所示。
由图7可知,为实现功率平衡,调制波的计算中包括附加控制模块,其输出占比较小,这导致调制波中存在高频脉动成分,不再是标准的正弦波。当子模块投入数的参考值接近整数时,采用floor函数对参考值Nref向下取整将导致整数投入数NSTEP产生波动,进而导致Si子模块开关频率的上升,如图11所示,Nref在整数附近的波动将导致阶梯数NSTEP在短时间内快速变化。
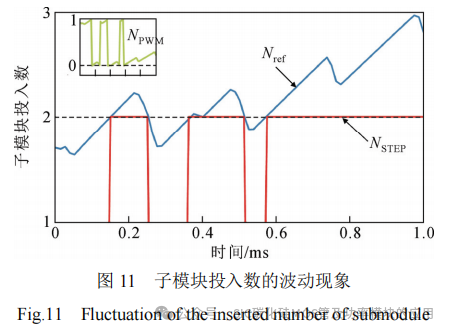
为解决这一问题,对阶梯数NSTEP进行采样,当值与前一采样时刻相等时,进行计数;与前一采样时刻不等时,若计数值达到n,则允许NSTEP变化,否则NSTEP保持不变。n的近似值为

式中:fSTEP为阶梯数变化频率;fs为采样频率。改进方案的子模块投入数如图12所示。
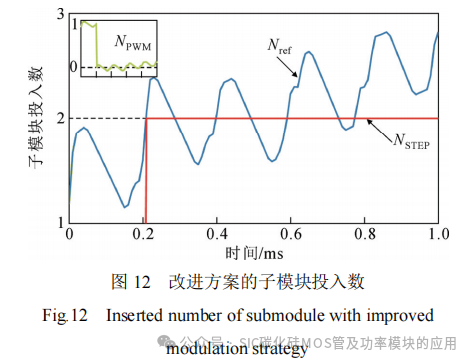
由图12可见,当Nref <NSTEP时,NPWM为负值,如绿线所示,此时使SiC子模块负投入。通过这种方案,解决了阶梯数短时间内快速波动的问题,同时又能保证阶梯数正常变化,维持波形质量。
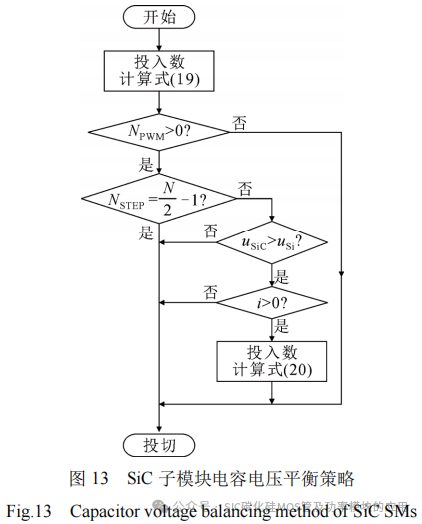
具体的SiC子模块电容电压平衡控制策略流程图如图13所示。其中,uSiC与uSi分别表示SiC子模块与Si子模块电容电压;i为桥臂电流。首先根据式(19)计算NSTEP与NPWM,若NPWM<0则跳过判断环节,SiC子模块进行负投入;若NSTEP未达到最大值,且uSiC低于平均电容电压,桥臂电流>0时,根据式(20)重新计算NPWM,使得SiC子模块负投入放电,除此之外均进行正投入。
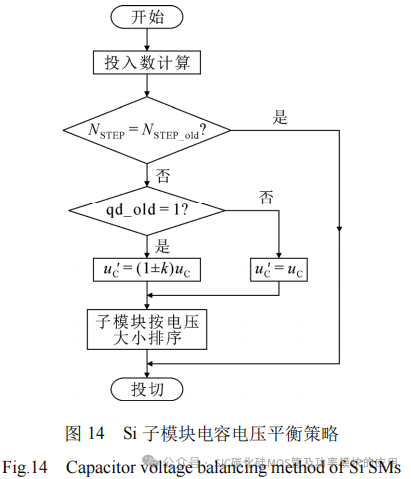
同时,Si子模块在阶梯数变化时采用增量排序的电容电压平衡控制策略,如图14所示。图中,NSTEP_old表示上一采样时刻的阶梯数,若阶梯数不变,则跳过排序,按上一采样时刻的顺序对子模块进行投切;qd_old表示子模块上一时刻的投切状态,1为投入;uC为子模块电容电压采样值;uC′为电压排序值;k为增量因子,用来调整子模块电容电压,增大投入子模块在下一时刻投入的概率。若上一时刻该子模块投入,当桥臂电流>0时,k取−0.2;桥臂电流<0时,k取0.2,以降低Si子模块的开关频率,并实现Si子模块的电容电压平衡。
利用该方法可以实现SiC子模块的自由控制以及子模块的电压平衡。所提出的电容电压平衡控制策略只在NSTEP发生变化时才对Si子模块重新排序,且Si子模块的开关频率不受SiC子模块的影响,大部分开关动作转移到SiC MOSFET上,大大降低了Si子模块的开关损耗。
4.实验验证

为了验证提出的改进FC-MMC方案的可行性,本文搭建了实验平台如图15所示,参数如表1所示,实验结果如图16所示。
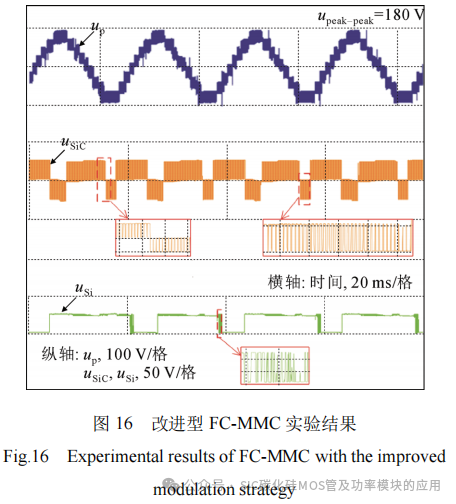
其中up为上桥臂电压;upeak-peak为桥臂电压峰峰值。实验采用PI控制,表2为控制回路Kp、Ki参数。SiC子模块工作在PWM模式,承担了大部分开关动作,端口电压在正、负和零之间快速切换,开关频率为9.38 kHz。当波形在基准线之下时,表示端口电压为负,此时SiC子模块进行负投入。而Si子模块工作在NLM模式,采用增量排序电容均压策略,工作状态为正投入或切除,仅在阶梯数变化时有少部分开关动作。
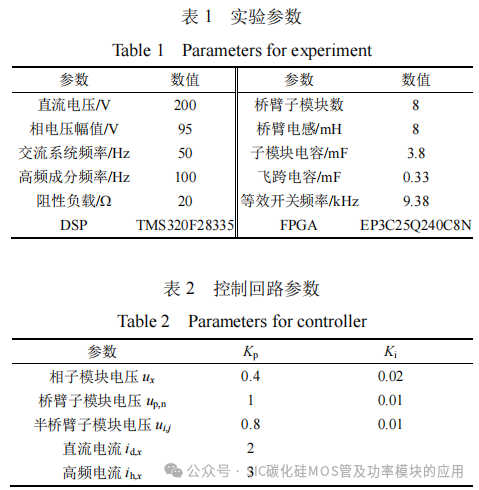
图17为传统FC-MMC对比实验结果,主电路参数与表1一致,uSM1与uSM2为子模块端口电压。由于采用载波移相调制,各子模块均工作在PWM模式,开关频率相同,工作状态在正投入和切除中快速切换,开关损耗较高。
图18为子模块电容电压波动对比,uC1为传统MMC子模块电容电压,采用NLPWM调制策略,PWM调制分散在各个子模块中,主电路参数与改进FC-MMC一致。同时,为保证对比实验变量统一,传统MMC仍采用增量排序的电容电压平衡控制策略,在阶梯数变化时对子模块重新排序。uC2为改进型FC-MMC电容电压。两种方案均采用增量排序的均压策略来降低开关频率,电容电压存在一定波动。将系统参数代入式(18),得到传统FC-MMC子模块电容电压波动为0.61 V,改进方案实验结果与其相近。由对比可知,改进型FC-MM的子模块电容电压控制在1 V之内,电压波动减小了约50%。
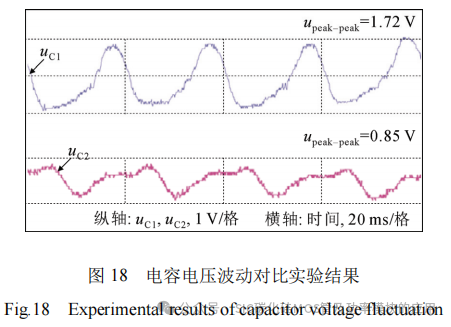
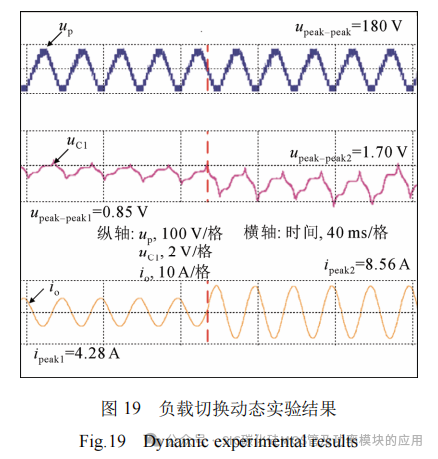
图19为电阻负载由20 Ω变为10 Ω动态实验结果。其中虚线为负载切换点,upeak-peak1、upeak-peak2分别为负载切换前后桥臂电压峰峰值,ipeak1、ipeak2分别为负载切换前后桥臂电流峰峰值。在负载减小一半后,子模块电容电压与输出电流均增大为之前的两倍,系统具有较好的动态性能。由于采用增量排序的均压策略来降低Si子模块的开关频率,电容电压存在轻微的波动。
5.改进方案损耗分析
为了验证采用新拓扑与调制方案的改进FC-MMC低损耗优势,本章首先给出了开关器件损耗表达式,接着基于PLECS进行损耗分析,对比了传统FC-MMC与改进FC-MMC功耗。其中传统FC-MMC子模块采用半桥拓扑。
开关器件的功率损耗主要包括导通损耗、开关损耗与驱动损耗。其中,驱动损耗占比较小,可忽略不计。导通损耗指通态下工作电流流经器件时,由于器件存在一定的导通电阻,导通压降不为零,进而产生的功率损耗,可由工作电流与导通压降乘积计算。导通损耗可以表示为
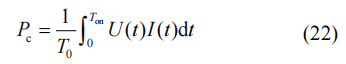
式中:T0为单位周期;Ton为一个周期内开关管导通时间;U(t)表示工作电流为I(t)时导通压降。根据器件数据手册可以得到导通压降U(t)与工作电流I(t)的关系,进而计算其导通损耗。同时,考虑到结温对导通电阻的影响,根据数据手册数据可以估算出不同结温下压降U与工作电流I的关系
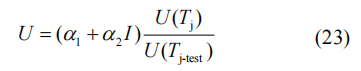
式中:Tj-test为数据手册中给出的结温;Tj为器件实际结温;α1、α2为根据数据手册电流电压关系函数拟合的系数。为提高表达式精度,可采用更高阶的函数进行拟合。
功率器件的导通和关断无法瞬时完成,存在电压与电流重叠的过程,由此产生的损耗称为开关损耗,包括开通损耗和关断损耗。开关损耗还受器件开关频率的影响,频率越高,开关损耗越大。单次开关动作造成的损耗E同样可以根据数据手册进行拟合,表达式为

式中α3、α4为拟合系数,考虑到结温与开关时刻截止电压变化的影响,开关损耗表达式修正为
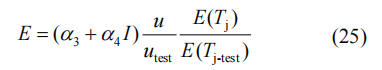
式中:utest为数据手册中给出的截止电压;u为器件实际的截止电压。由于子模块电容电压存在波动,因此在计算开关损耗时需要考虑电压的变化。对一个周期内的开关损耗进行求和,除以单位时间得到平均开关损耗,表达式Ps为
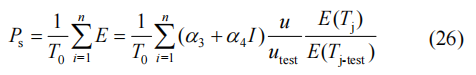
其中n为单位周期内器件开关次数。
对于开关器件反并联的整流二极管,其功率损耗主要包括通态损耗、开通损耗、截止损耗与反向恢复损耗。其中,开通损耗与截止损耗占比较小,可忽略不计。通态损耗的产生机理与IGBT类似。二极管关断时PN结存储的电荷需被清除而产生较大的反向恢复电流,由此产生的损耗称为反向恢复损耗。两种损耗的表达式均可类比开关器件,根据数据手册进行函数拟合。
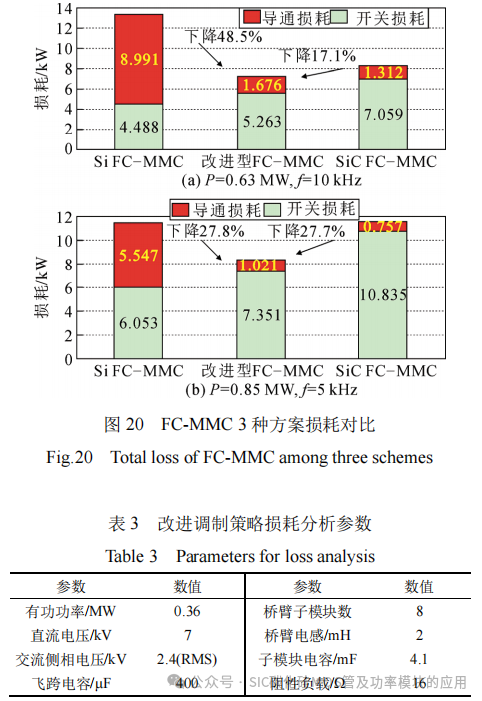
基于PLECS的损耗对比结果如图20所示,进行了额定功率P=0.63 MW、等效开关频率f=10 kHz与额定功率P=0.85 MW、等效开关频率f=5 kHz两组对比仿真,主电路参数如表3所示。其中,Si IGBT采用ABB的5SNG0300Q170300,SiC MOSFET采用CREE的CAS300M17BM2。由于改进型FC-MMC采用Si IGBT与SiC MOSFET混合结构,与完全基于Si IGBT的FC-MMC具有相似的导通损耗特性,与完全基于SiC MOSFET的FC-MMC具有相似的开关损耗特性。在大功率场合,SiC MOSFET具有更高的导通压降,其导通损耗显著高于Si IGBT;在高开关频率场合,Si IGBT开关损耗大幅提升。
对于改进型FC-MMC,开关动作主要集中于SiC MOSFET,虽然由于Si IGBT的少量开关动作其开关损耗略高于完全基于SiC MOSFET的FC-MMC,但由于主电路中功率器件大部分为SiIGBT,其导通损耗大幅减小,因此总损耗最低。且随着额定功率与等效开关频率的提升,改进方案较两种传统方案的损耗优势更为明显。在P=0.63MW、f=10kHz工况下,与传统FC-MMC的两种方案相比,改进型FC-MMC的功率损耗分别降低了48.5%和17.1%;在P=0.85MW、f=5kHz工况下,其功率损耗分别降低了27.8%与27.7%。
6.结论
1)提出了一种新型FC-MMC拓扑,该拓扑每个桥臂包括两个SiC子模块及多个Si子模块,SiC子模块采用基于SiC MOSFET的全桥拓扑,Si子模块采用基于Si IGBT的半桥拓扑,与完全基于SiC MOSFET的变换器相比显著降低了成本。
2)提出了相应的调制策略,SiC子模块工作在PWM模式,Si子模块工作在NLM模式,将大部分开关动作集中在SiC MOSFET上,充分利用了SiC MOSFET开关损耗低与Si IGBT导通损耗低的优势,实现了总损耗的优化。
3)在新调制策略中,利用SiC全桥子模块的负投入能力实现子模块的电容电压平衡,同时增加延时模块,解决了调制波波动导致的阶梯数波动问题。
4)通过对比实验,验证了所提改进方案的可行性以及电容电压波动抑制效果,并通过损耗分析,说明了该方案低功率损耗的优势。

