摘 要:碳化硅金属–氧化物半导体场效应晶体管(SiC metal-oxide-semiconductor field-effect transistor, SiC MOSFET)在高速开关中引起的桥臂串扰和栅极电压振荡严重制约了其开关速度。针对已提出的基于推挽式电容辅助电路(push-pull-capacitor auxiliary circuit, PPCAC)的SiC MOSFET驱动工作过程进行了进一步的分析。结合分析,将SiC MOSFET桥臂串扰以及漏源电压振荡引起的栅源电压振荡2个问题归一化,通过推挽电容充放电时刻以及桥臂串扰约束,提出了一种推挽电容参数设计方法。通过该设计方法,可使得PPCAC在抑制SiC MOSFET桥臂串扰与栅源电压振荡的基础上,改善其开通关断速度。实验结果验证了所提出设计的有效性。
关键词:SiC MOSFET;桥臂串扰;栅源电压振荡;推挽式电容辅助电路;开关速度
0.引言
碳化硅金属−氧化物半导体场效应晶体管(SiCmetal-oxide-semiconductor field-effect transistor, SiC MOSFET)具有阻断电压高、开关速度快、导通电阻低、耐高温等优点,可用于设计具有更高效率、更高功率密度的电能变换装备。但因SiC MOSFET自身的寄生参数、功率回路及驱动回路的寄生电感等非理想因素引起的桥臂串扰与振荡等负面影响,导致SiC MOSFET桥臂电路在高速开关过程中容易发生故障。桥臂电路是一种常用的电路结构,含有2个串联且互补导通的开关器件,而桥臂串扰是指当桥臂电路中某一个SiC MOSFET高速开通或者关断时,同一桥臂电路的另一个SiC MOSFET的漏源电压变化率很大,分别在米勒电容上产生很大的米勒电流,进而抬高或者拉低栅极电位。由于SiC MOSFET的开通阈值电压较小,桥臂正向串扰极有可能使关断状态下的SiC MOSFET误开通,导致短路故障。负向串扰可能导致栅源电压低于其栅极最大负压,使器件性能退化或损坏。
目前抑制桥臂串扰的方案主要分为2类:无源抑制和有源抑制。无源抑制方案通过增大驱动电阻或栅源并联电容来实现,缺点是会增加开关损耗或降低开关速度。有源抑制方案又分为2类:一类通过辅助电路预置相应的电压等级来抑制串扰,但该方案电路结构较复杂,且难以准确判断开关过程中串扰的极性。文献[10]提出了一种具有电平移位功能的高速负压驱动器,通过降低负压与米勒钳位共同作用来抑制串扰。另一类是在桥臂串扰产生阶段,通过设置辅助电路在栅源间并入大电容,从而抑制桥臂串扰,但该方案通常需要额外的控制信号,增加了驱动控制的复杂度。文献[11-12]在器件栅源极之间添加了一条由辅助MOS管与辅助电容串联的支路,辅助MOS管需要额外的驱动信号,增加了控制难度;文献[13]则在器件栅源极之间并联三极管、二极管和电容组成的辅助电路。
此外,电路中存在寄生参数,在器件开关过程中,漏源电压会出现振荡并耦合至驱动回路,引起栅源电压振荡,导致器件误动作或负压击穿。为减小功率回路寄生电感,在变换器设计时通常采用层叠式复合母排,或采用垂直式PCB环路设计使正反面的换流路径尽可能交叠,从而抵消磁场影响,最小化杂散电感。文献[17]在驱动回路中串联具有适当阻抗特性的磁珠,对漏源电压振荡引起的栅源电压振荡也有一定程度的抑制。实际上,漏源电压振荡所引起栅源电压振荡和桥臂串扰产生机理一致,都是由漏源电压变化通过米勒电容耦合至驱动回路,引起栅源电压变化。因此,栅源电压振荡也可以通过增大驱动电阻或栅源并联电容来抑制。
为抑制桥臂串扰和漏源电压振荡引起的栅源电压振荡,笔者在前期工作中提出了一种基于推挽式电容辅助电路(push-pull-capacitor auxiliary circuit,PPCAC)的SiC MOSFET驱动,该方案可在抑制桥臂串扰与栅源电压振荡的基础上,优化开关速度,且不需额外控制信号。然而,以上文献对PPCAC驱动分析并不深入,所采用参数设计方法也不尽合适。进一步分析笔者之前所提出的PPCAC驱动,将桥臂串扰以及漏源电压振荡引起的栅源电压振荡2个问题归一化,通过推挽电容充放电时刻以及桥臂串扰约束,提出一种推挽电容参数设计方法。论文首先给出桥臂串扰与漏源电压振荡引起的栅源电压振荡产生机理,接着分阶段分析PPCAC驱动工作过程,对PPCAC推挽电容参数进行设计,最后实验验证了所提出设计的有效性。
1.桥臂串扰与栅源电压振荡分析
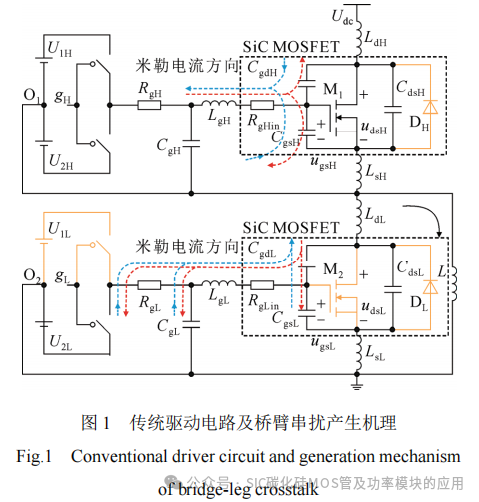
基于传统驱动电路的桥臂电路如图1所示。其中,M1为桥臂上管,M2为桥臂下管,虚线框内为SiC MOSFET器件模型,CgdH、CgsH、CdsH分别为上管米勒电容、栅源寄生电容、漏源寄生电容,CgdL、CgsL、CdsL分别为下管米勒电容、栅源寄生电容、漏源寄生电容,RgHin与RgLin为栅极内部电阻,DH和DL为反并联二极管;LgH、LdH和LsH分别为上桥臂SiC MOSFET的栅极、漏极和源极寄生电感,LgL、LdL和LsL分别为下桥臂SiC MOSFET的栅极、漏极和源极寄生电感,RgH和RgL分别为桥臂上、下管驱动电路中的驱动电阻,CgH和CgL分别为桥臂上、下管驱动电路中的栅源并联电容;gH和gL为驱动控制信号;ugsH和udsH分别为上管栅源电压、漏源电压,ugsL和udsL分别为栅源电压、漏源电压,U1H、U2H和U1L、U2L为驱动电源。
1.1桥臂串扰产生原理
图2给出了SiC MOSFET的典型开关过程。
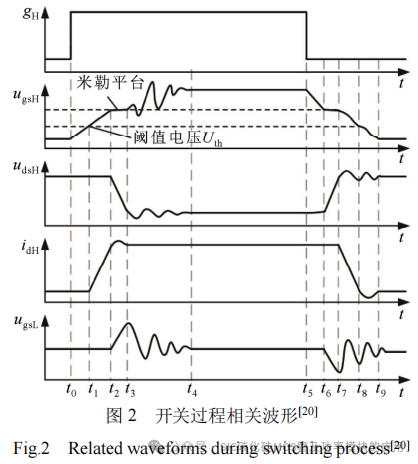
正向串扰发生在图2中的t2~t3阶段,下管漏源电压udsL快速上升,使得下管米勒电容CgdL两端电压上升速率很大,进而出现一个较大的米勒电流流过电容CgdH,幅值为CgdLdugdL/dt,该米勒电流分别流向下管栅源寄生电容CgsL、下管栅源并联电容CgL和驱动电阻RgL,使下管栅源电压ugsL上升,严重时正向串扰会引起下管误开通,导致桥臂短接。同理,负向串扰发生在图2中的t6~t7阶段,下管米勒电容产生的米勒电流使下管栅源电压ugsL下降,严重时会超过SiC MOSFET栅源最大负压,导致负压击穿。
1.2栅源电压振荡产生机理
在t3~t4阶段,理想情况下,上管栅源电压ugsH继续上升至驱动电源电压,下管栅源电压ugsL由串扰阶段的被抬高状态跌落回到低电平,开通过程结束。实际上,在t2~t3阶段,上管漏源电压下降到0 V,下管漏源电压达到母线电压后,受换流回路寄生电感的影响,上、下管漏源电压发生振荡,上管漏源电压振荡在上管米勒电容CgdH上产生较大的CgdH dugdH/dt,下管漏源电压振荡在下管米勒电容CgdL上产生较大的CgdL dugdL/dt,分别对上、下管栅源电压产生干扰。因此,栅源电压也发生振荡。t7~t9阶段同理。该振荡现象有可能使栅源电压ugs振荡高于开通阈值电压,低于栅源所能承受的最大负压。
综上,当SiC MOSFET高速开关时,受换流回路寄生电感和SiC器件寄生参数的影响,桥臂电路中各开关管的漏源电压发生变化,通过米勒电容耦合至驱动回路,进而引起桥臂串扰和栅源电压振荡。
2.基于PPCAC的SiC MOSFET驱动工作过程分析
通过以上分析,增大驱动电阻或栅源并联电容可以抑制桥臂串扰与栅源电压振荡,但同时会造成SiC MOSFET开关速度减慢。综合考虑桥臂串扰与栅源电压振荡抑制效果、开关速度、控制复杂度等因素,作者在前期工作中提出了一种基于PPCAC的驱动,可在不影响SiC MOSFET开关速度的情况下,有效地抑制桥臂串扰与栅源电压振荡。
2.1基于PPCAC的驱动电路
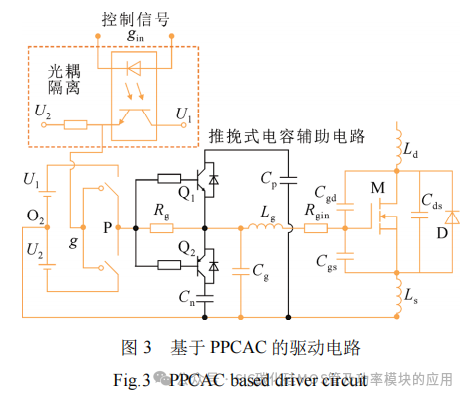
图3给出了基于PPCAC的驱动电路原理图,在传统驱动电路基础上增加了推挽式电容辅助电路,包括NPN三极管Q1和PNP三极管Q2,辅助电容Cp、Cn。其中三极管Q1和Q2基极控制信号共同接入P点,其控制信号与驱动控制信号g等效,因此无需额外控制信号。文献[13]中辅助电路也包括2个并联支路,但每个支路采用独立的电容,且二极管和三极管反并联接,稳态工作时,2个电容电压为驱动电源电压。
2.2串扰与振荡抑制机理
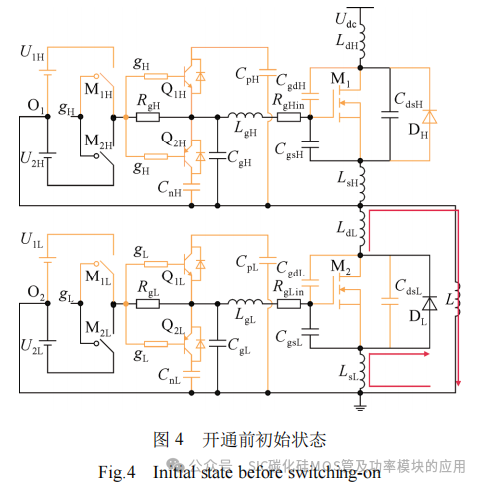
以桥臂上管动作、下管保持关断为例,根据图2中的相关波形,分阶段分析PPCAC驱动方案的开关过程。图4为上管开通前的初始状态,桥臂上下管均保持关断,NMOS管M1H、M1L和三极管Q1H、Q1L、Q2H、Q2L都处于关断状态,PMOS管M2H和M2L处于开通状态,上管栅源电压ugsH为驱动电源电压U2H,负载电流iL经反并联二极管DL续流。
开通过程如下文所述。
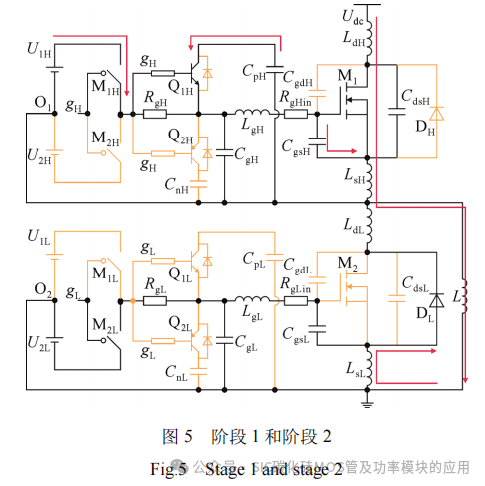
阶段1和阶段2(t0~t2):如图5所示,t0时刻,M1的驱动信号gH变为高电平,M1H开通,M2H关断。驱动电源U1H通过电阻RgH、RgHin给电容CgH、CgsH充电,RgH上产生压降使三极管Q1H的基极与发射极电位差大于0.7 V,Q1H开通,推挽电容CpH并联到上管栅源极之间,CpH储存的能量与U1H同时向CgsH和CgH充电,ugsH从负压U2H开始快速上升,上升至阈值电压Uth时,即t1时刻,上管M1开通,流过M1的漏极电流idH线性上升。反并联二极管DL仍对负载电流iL续流,下管漏源电压udsL=0 V。
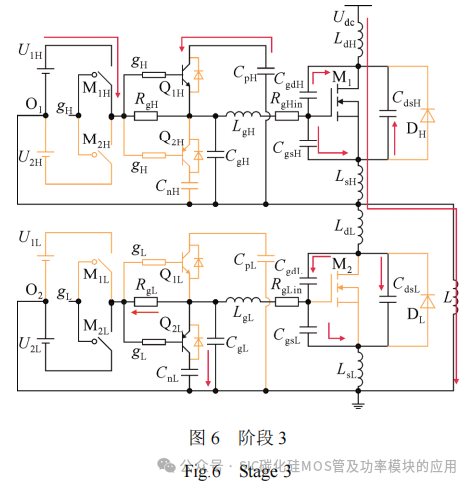
阶段3(t2~t3):如图6所示,下管M2漏源电压udsL迅速上升,米勒电容CgdL两端电压ugdL近似线性上升,则米勒电流igdL大小为CgdLdugdL/dt,流向CgsL、CgL、RgL及驱动电源U2L,同时RgL上产生的压降使三极管Q2L发射极与基极之间电位差大于0.7 V,Q2L开通,下管推挽电容CnL并到栅源极之间,米勒电流igdL通过CnL分流,抑制下管栅源正向串扰。同时,上管M1的米勒电容CgdH两端电压线性下降,产生大小为CgdHdugdH/dt的米勒电流igdH,该米勒电流由驱动电源U1H和推挽电容CpH上储存的能量提供。随着推挽电容CpH不断放电,电压逐渐下降至某一特定值时,放电结束,转而通过Q1H反并联二极管进入充电状态,等效于增大并联栅源电容,此时驱动电源U1H开始同时给CgH、CpH与CgsH供电,CgH、CpH与CgsH两端电压开始同时上升。这一阶段,推挽电容CpH完成充放电转变。
阶段4(t3~t4):这一阶段的栅源电压ugsH和ugsL仍在振荡,当上管栅源电压ugsH和推挽电容CnH两端电压达到驱动电源电压U2H后,上管完全开通。
关断过程分为4个阶段,如下文所述。
上管关断前的初始状态,此时上管M1完全开通,上管栅源电压ugsH为驱动电源电压U1H,M1H处于开通状态,M2H、Q1H、Q2H处于关断状态。CnH、CnL两端电压分别为U2H和U2L,CpH、CpL两端电压分别为U1H和U1L。
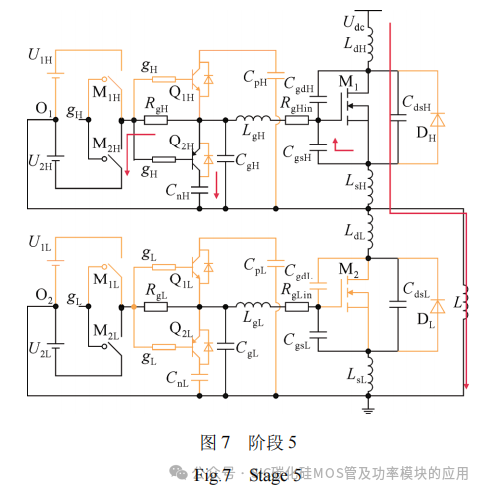
阶段5(t5~t6):如图7所示,t5时刻,M1的驱动信号gH变为低电平,M2H开通,M1H关断。电容CgH、CgsH通过电阻RgH向驱动电源U2H放电,RgH上的压降使三极管Q2H发射极与基极的电位差大于0.7 V,Q2H开通,推挽电容CnH并联到上管栅源极之间,为CgH、CgsH提供放电支路,CnH处于充电状态,栅源电压ugsH快速下降。此时桥臂电路状态保持不变。
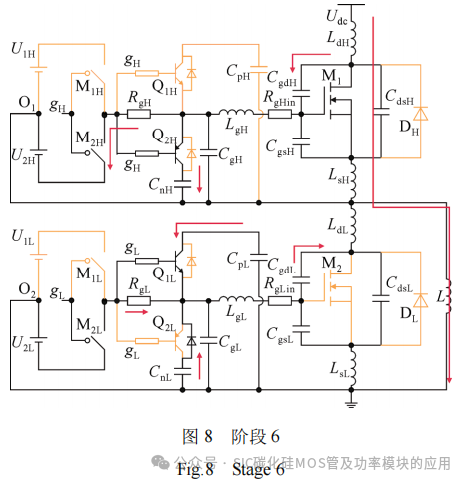
阶段6(t6~t7):如图8所示,下管M2漏源电压udsL迅速上升,米勒电容CgdL两端电压ugdL近似线性上升,则米勒电流igdL大小为CgdLdugdL/dt,由驱动电源U2L、电容CgL、电容CgsL提供,RgL上产生压降使得三极管Q1L的基极与发射极的电位差大于0.7 V,Q1L开通,推挽电容CpL并联在栅源极之间,推挽电容CnL两端电压与PNP三极管Q2L发射极的电位差大于与三极管Q2L反并联的二极管导通压降,因此,推挽电容CnL也并联在栅源极之间,米勒电流通过推挽电容CnL和CpL分流,抑制了下管栅源负向串扰。值得注意的是,由于三极管和二极管存在导通电阻,当推挽电容CpL和CnL都并入栅源之间时,栅源电压并不会被其初始电压钳位。同时,上管M1的米勒电容CgdH两端电压快速线性上升,产生大小为CgdHdugdH/dt的米勒电流,由于三极管Q2H开通,该米勒电流分别流向推挽电容CnH和驱动电源U2H。
随着推挽电容CnH不断充电,其电压逐渐上升,当上升到一定电压值时,CnH不再充电,转而通过Q2H反并联二极管进入放电状态,等效于增大并联栅源电容,此时电容CnH、CgsH、CgH同时向驱动电源U2H放电,CnH、CgsH、CgH两端电压开始同时下降。推挽电容CnH完成充放电转变。可以有效缩短t5~t7的时间,进而提高SiC MOSFET的关断速度。
阶段7(t7~t8):上管关断并承受直流母线电压,下管漏源电压下降为0 V,受SiC MOSFET寄生电感及功率回路寄生电感等非理想因素的影响,桥臂上管、下管漏源电压发生振荡,分别通过米勒电容耦合至驱动回路中,使得栅源电压发生振荡。这一阶段,由于振荡过程产生不同方向的米勒电流,上管Q2H及其反并联二极管、下管Q2L及其反并联二极管交替导通。由于漏源电压振荡产生的米勒电流小于串扰发生阶段的米勒电流,并且此时上管推挽电容CnH、下管推挽电容CnL已并联在栅源极之间,因此,可以有效地抑制栅源电压振荡。
阶段8(t8~t9):这一阶段的栅源电压ugsH和ugsL仍在振荡,当上管栅源电压ugsH和推挽电容CnH两端电压达到驱动电源电压U2L后,上管关断结束。
3 .PPCAC推挽电容参数设计
3.1问题归一与设计约束建立
由2.2节分析可知:t0~t3阶段,桥臂上管的推挽电容CpH并在栅源极之间,工作在放电状态,其存储的能量能够给栅源寄生电容CgsH充电,从而提高SiC MOSFET的开通速度;t3~t4阶段,推挽电容CpH转变为充电状态,并入栅源之间,等效于增大并联栅源电容,抑制由漏源电压振荡导致的栅源电压振荡;t2~t4阶段,推挽电容CnL并在下管栅源极之间,对下管米勒电流进行分流,抑制了下管的桥臂串扰和栅源电压振荡。
PPCAC的参数设计主要为上、下推挽电容值。综上所述,推挽电容值设计需考虑以下因素:(1)开通过程中,桥臂上管推挽电容CpH充放电时刻,上管栅源电压振荡及下管栅源电压串扰与振荡幅值;(2)关断过程中,上管推挽电容CnH充放电时刻,上管栅源电压振荡以及下管栅源电压串扰与振荡幅值。考虑到推挽式电容电路的对称性、开通关断过程近似对称性,本文上、下推挽电容值取值相同,且仅研究上管开通过程。由于振荡阶段漏源电压变化率小于串扰发生阶段的漏源电压变换率,因此栅源电压振荡幅值小于串扰电压幅值,进而这2个问题可以归一化,通过串扰电压幅值约束设计来进行抑制。最终,推挽电容值设计约束归结为:(1)开通过程中上管推挽电容CpH充放电时刻;(2)开通过程中下管栅源串扰电压幅值。
3.2开通过程中上管推挽电容充放电时刻设计
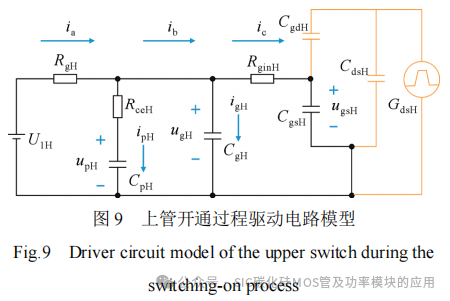
忽略t2~t3阶段米勒电流及驱动回路寄生电感影响,图9为上管驱动电路模型,图中RceH为三极管饱和导通电阻,ia、ib、ic为各支路电流,ipH为推挽电容CpH上的电流,igH为栅源并联电容CgH上的电流。当电流ia=ib、即ipH=0时,推挽电容CpH由放电转为充电,驱动电源U1H同时给推挽电容CpH、栅源并联电容CgH和栅源寄生电容CgsH供电,CpH、CgH和CgsH两端电压同时上升。
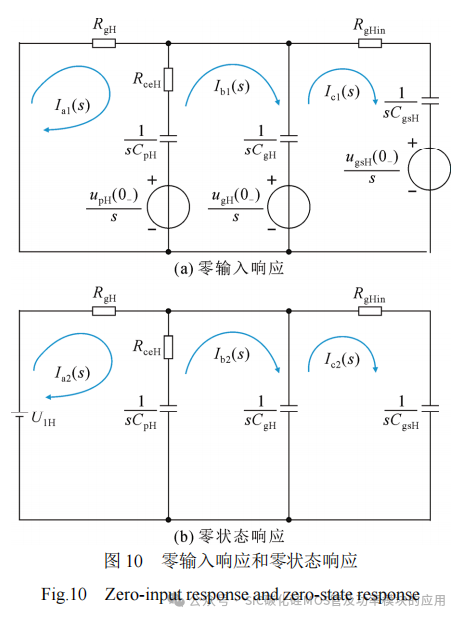
通过拉氏变换,得到复频域模型如图10所示,图中Ia1、Ib1、Ic1为零输入响应模型的网孔电流,Ia2、Ib2、Ic2为零状态响应模型的网孔电流。根据叠加定理,分别计算零输入响应和零状态响应,进而得到全响应,通过拉氏逆变换即可得到各变量的时域表达式。本节需计算推挽电容CpH上的电流ipH,当ipH=0时,推挽电容CpH进行充放电转换。
根据图10列写回路电流方程式,可求解出电流ia、ib、ipH、CpH两端电压upH和CgsH两端电压ugsH的时域表达式。由于篇幅限制,具体表达式及推导过程在附录A中给出,根据式(A6)和式(A7),可作出各变量变化曲线图,如图11所示。
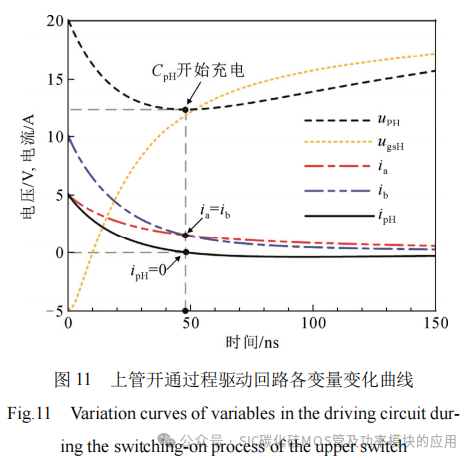
表达式(A6)和式(A7)中的参数参照CREE公司C2M0040120D型号的SiC MOSFET,栅源寄生电容CgsH为1 883 pF,栅漏寄生电容CgdH为10 pF,漏源寄生电容CdsH为140 pF,栅极内阻RgHin为1.8 Ω。驱动开通电压U1H为20 V,驱动关断电压U2H为–5 V。取推挽电容CpH为10 nF、栅源并联电容CgH为10 nF、驱动电阻RgH为5 Ω,RceH为5 Ω。
从图11中可以看出,栅源寄生电容CgsH两端电压ugsH从U2H开始逐渐上升,推挽电容CpH两端电压upH从U1H开始逐渐下降,当电流ia=ib、即ipH=0时,推挽电容CpH由放电转为充电,推挽电容两端电压upH与栅源电压ugsH同步上升。
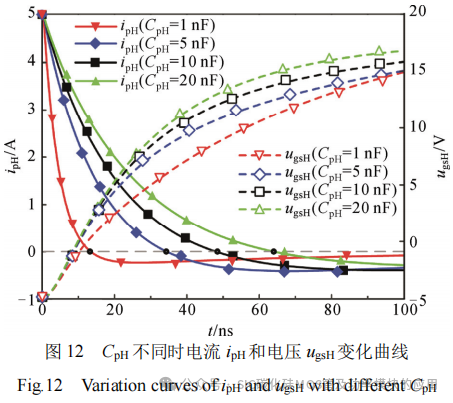
图12对比了不同推挽电容CpH时电流ipH和电压ugsH变化曲线。由图可知,随着推挽电容值CpH增大,其存储能量增大,进而充放电转换时刻后移。同时,随着推挽电容CpH增大,ugsH上升变快,表示器件开通速度变快。开通过程中,桥臂上管栅源电压振荡发生在t3时刻以后,即串扰阶段以后,实际设计中,上管推挽电容CpH充放电转换时刻可设置在t2~t3阶段,如2.2节阶段3分析过程。本文初步设计推挽电容为10 nF,如图12,该容值对应充放电转换时刻为48 ns左右,此时所对应的栅源寄生电容两端电压ugsH约为12.5 V。该推挽电容值为初步设计,实际应用时可结合测试结果调整。
3.3开通过程下管栅源串扰电压幅值设计
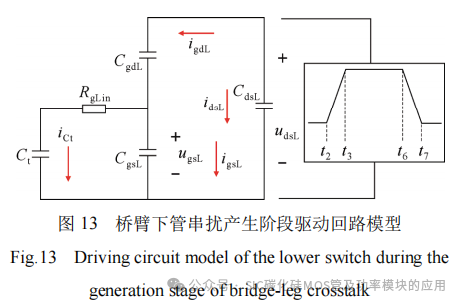
忽略寄生电感和三极管导通电阻的影响,t2~t3阶段下管驱动回路的数学模型如图13所示,根据基尔霍夫定律得
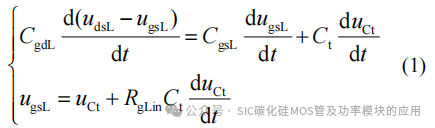
式中:桥臂下管栅源间并联总电容Ct=CnL+CgL;uCt为其两端电压。
设直流母线电压为Udc,t2~t3阶段下管漏源电压上升时间tr为Δt,认为开关过程中漏源电压线性变化,因此漏源电压变化率dudsL/dt近似为恒定值Udc/Δt。由2.2节可知,下管漏源电压上升时,米勒电流流向栅源寄生电容CgsL,下管漏源电压升到直流母线电压时,串扰达到最大值,因此,t=Δt时,dugsL/dt=0。由式(1)可得串扰电压Δu与下管栅源间并联总电容C的关系
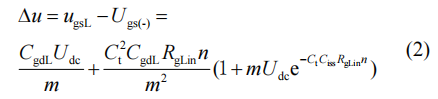
式中:Ct=CnL+CgL;Ciss=CgsL+CgdL;m=Ct+Ciss;n=Udc/Δt;Ugs(-)为SiC MOSFET关断时栅源电压,即U2H。
为了避免开通过程中正向串扰导致器件误导通及关断过程中负向串扰导致器件负压击穿,串扰电压Δu需满足式(3)中的条件。
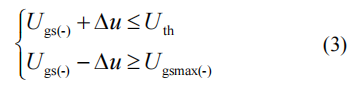
式中,Ugsmax(-)为SiC MOSFET允许的最大负压。联立式(2)与式(3)可确定推挽电容CnL的取值范围。
以CREE公司型号为C2M0040120D的SiC MOSFET为例,其阈值电压Uth为2.6 V,功率开关器件允许的最大负压Ugsmax(-)为–10 V。取直流母线电压Udc为600 V,串扰电压Δu与下管栅源间并联总电容Ct的关系如图14所示。
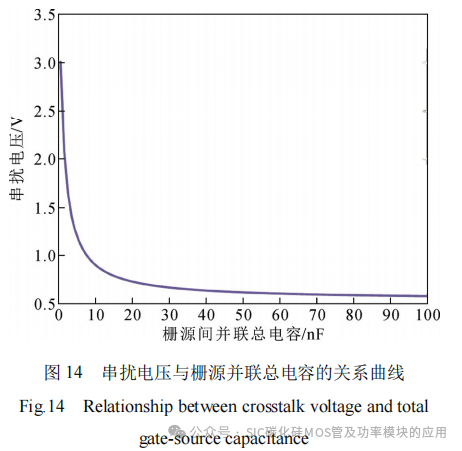
从图14可以看出,当栅源间并联总电容Ct>20 nF时,串扰电压曲线趋于平缓,抑制效果减弱。因此,栅源间并联总电容Ct设计为20 nF,CnL取10 nF,CgL取10 nF,此时,串扰电压Δu约为0.75 V,满足式(3)条件。
4. 设计验证与分析
4.1仿真验证
首先在LTspice中搭建双脉冲测试仿真模型,对所提出的PPCAC推挽电容参数设计方法进行验证。仿真模型中SiC MOSFET器件采用CREE官方网站所提供的C2M0040120D模型,其余器件参数与工作条件如表1所示。为避免篇幅过长,本节仿真验证部分仅给出开通过程的仿真结果,在4.2节实验验证中同时给出开通和关断过程的实验结果。
采用基于PPCAC的驱动电路及所设计的推挽电容参数,图15给出桥臂上管开通时,推挽电容CpH、CnL两端电压的仿真波形。
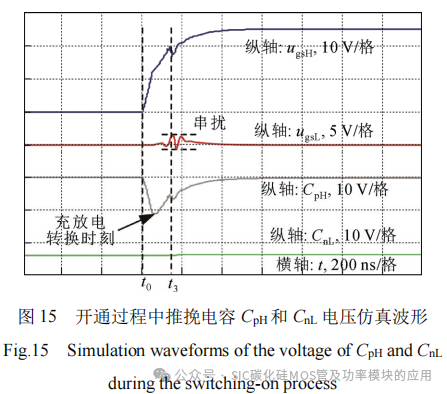
从图15可以看出,上管推挽电容CpH的电压在t0时下降,经过50 ns后开始上升,表明其在50 ns时由放电状态转变为充电状态,与3.2节中所设计的推挽电容充放电转换时刻48 ns相一致。
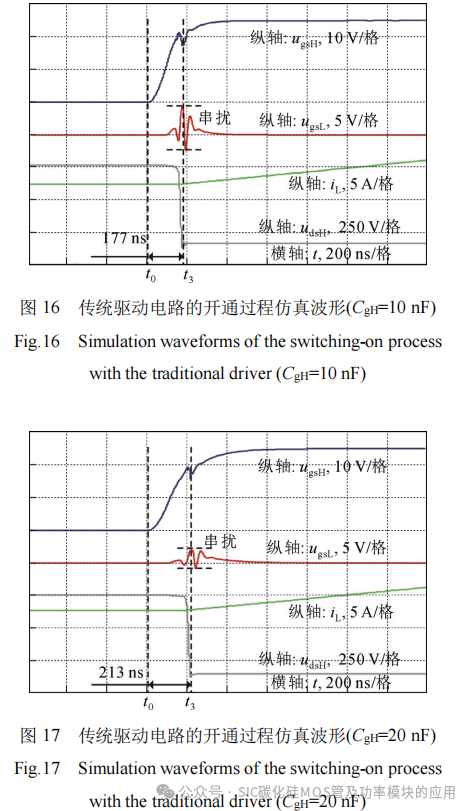
图16和图17分别给出了传统驱动电路中栅源并联电容为10 nF和20 nF时的开通过程仿真结果。图18给出了基于PPCAC的驱动电路的开通过程仿真结果,基于PPCAC的驱动电路的栅源并联电容为10 nF,推挽电容为10 nF。图16中,栅源并联电容为10 nF,传统驱动电路的开通时间约为177ns。图17中,栅源并联电容为20 nF,传统驱动电路的开通时间约为213 ns。可以看出,增大栅源并联电容,桥臂串扰得到明显抑制,但器件开通速度变慢。
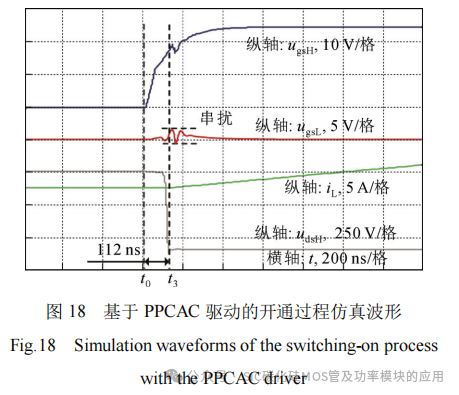
从图18可以看出,基于PPCAC的驱动电路开通时间约为112 ns,和图16中的情况相比,其开通时间下降约50 ns,这是由于桥臂上管推挽电容CpH在初始阶段进行放电,加快了上管栅源两端电压上升速度。和图17相比,其桥臂串扰抑制效果基本一致,这是由于串扰发生阶段,桥臂下管推挽电容CnL并联在下管栅源两端,因此栅源间等效并联电容为20 nF,和图17中情况相同。
4.2实验验证
为进一步验证所提出的PPCAC推挽电容参数设计方法抑制桥臂串扰和栅源电压振荡以及改善开关速度的效果,本文在两电平变换器测试平台上进行SiC MOSFET双脉冲实验,如图19所示。

本文使用CREE公司型号为C2M0040120D的SiC MOSFET,推挽式电容辅助电路选择集成了NPN和PNP三极管的芯片ZXGD3004E6,反并联二极管选择肖特基二极管DB2230600L,驱动芯片选择英飞凌的1ED020I12-F2,驱动电源采用Murata的MGJ2D052005SC芯片,能够为驱动电路及推挽电容式辅助电路提供+20 V/–5 V电源,满足设计要求。推挽电容设计为CpH=CnH=CpL=CnL=10 nF,电路中其他相关参数及工作条件如表1所示。
采用基于PPCAC的驱动电路以及所设计的推挽电容参数,图20给出桥臂上管开通时,推挽电容CpH、CnL两端电压的实验波形。
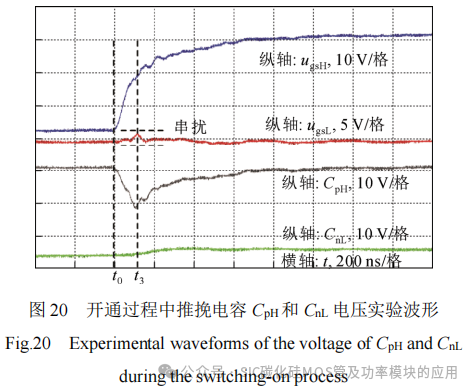
由图2可知,器件开通过程中正向串扰电压最大值位于t3时刻。从图20可以看出,上管推挽电容CpH电压在靠近t3时刻左侧附近的某一时刻开始上升,表明其在该时刻由放电状态转变为充电状态。同时,在正向串扰发生阶段,下管推挽电容CnL并在下管栅源两端,理论上,其电压值应和栅源电压一致,但由于三极管Q2L存在一定的饱和导通压降,推挽电容CnL两端电压略微上升。需要注意的是,在图11中,上管推挽电容CpH充放电转换时刻在48 ns左右,而从图20中可以看出,该充放电转换时刻在100 ns左右,通过分析可知,该误差主要与辅助电路中三极管Q1H的饱和导通电阻密切相关。
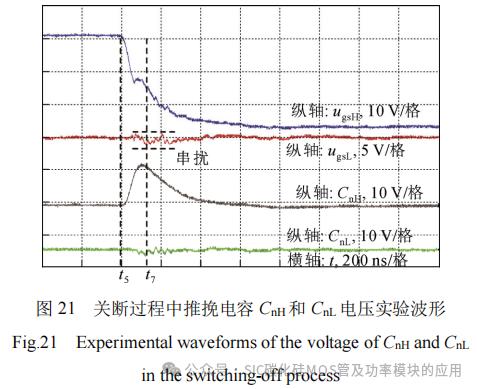
同理,图21给出桥臂上管关断时推挽电容CnH和CnL两端电压的波形。由图2可知,在器件开通过程中,负向串扰电压最大值位于t7时刻。从图21可以看出,上管推挽电容CnH电压在靠近t7时刻左侧附近的某一时刻开始下降,表明其在该时刻由充电状态转变为放电状态。在负向串扰发生阶段,下管推挽电容CnL并在下管栅源两端,理论上其电压值应和栅源电压一致,但由于三极管存在一定的饱和导通压降,推挽电容CnL两端电压降幅不明显。同样地,在关断过程中,三极管Q2H的饱和导通特性也引起上管推挽电容CnH充放电转换时刻误差。
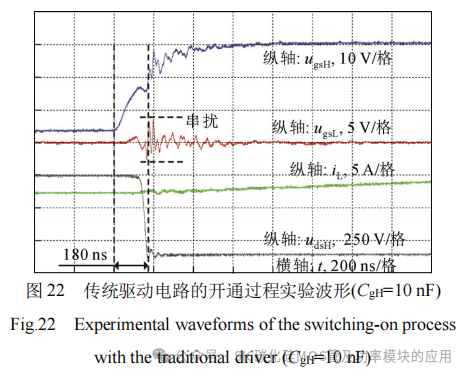
图22和图23分别给出了传统驱动电路中栅源并联电容为10 nF和20 nF时的开通过程实验波形,图24给出了PPCAC驱动电路的开通过程实验波形,此时PPCAC驱动电路的栅源并联电容为10 nF,推挽电容为10 nF。2种驱动电路驱动电阻均为5 Ω。
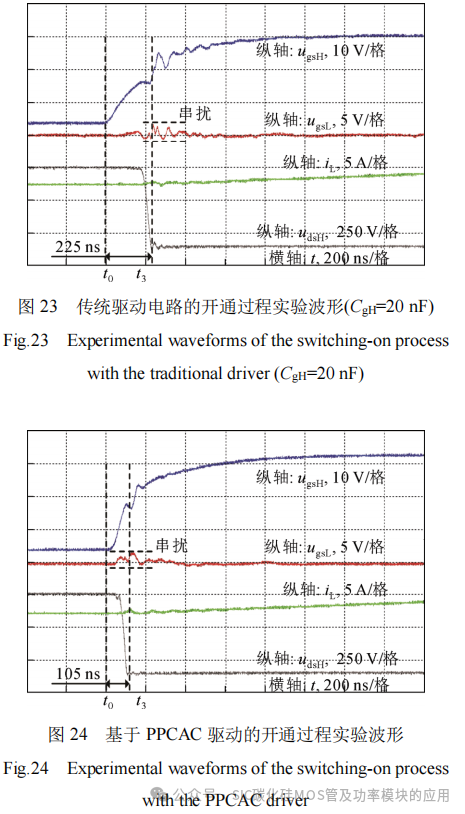
由实验结果可知,当栅源并联电容为10 nF时,传统驱动电路的开通时间约为180 ns,与图16中的仿真结果基本一致。当栅源并联电容为20 nF时,传统驱动电路的开通时间约为225 ns,与图17中的仿真结果基本一致。可以看出,增大栅源并联电容,器件开通速度变慢,但桥臂串扰得到明显抑制。而从图24可以看出,PPCAC驱动电路开通时间约为105 ns,与图18中的仿真结果基本一致。和图22情况相比,其开通时间下降约为41.6%,这是由于桥臂上管推挽电容CpH在初始阶段进行放电,加快了上管栅源两端电压上升。和图25相比,其桥臂串扰抑制效果基本一致,这是由于在串扰发生阶段,桥臂下管推挽电容CnL并联在下管栅源两端,因此栅源间等效并联电容为20 nF,和图23相同。
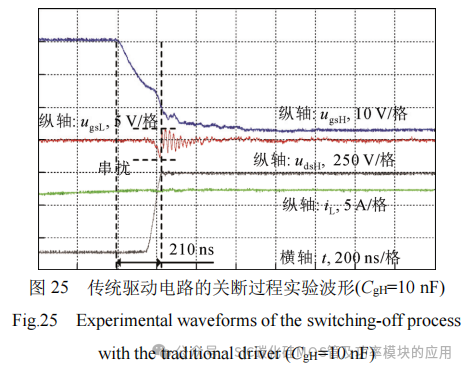
图25和图26分别给出了传统驱动电路中栅源并联电容为10 nF和20 nF时的关断过程实验波形,图27给出了基于PPCAC驱动电路的关断过程实验波形,此时PPCAC驱动电路的栅源并联电容为10nF,推挽电容为10 nF。门极驱动电阻仍均为5 Ω。
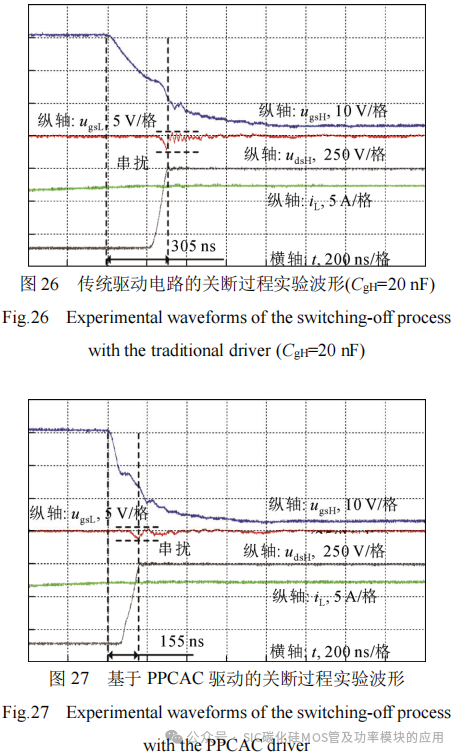
由实验结果可知,当栅源并联电容分别为10 nF和20 nF时,传统驱动电路的关断时间分别为210 ns和305 ns。可以看出,增大栅源并联电容,器件关断速度变慢,但桥臂串扰得到进一步抑制。而从图27可以看出,PPCAC驱动电路关断时间约为155 ns,和图25相比,关断时间下降约为26.2%,这是由于桥臂上管推挽电容CnH在初始阶段进行充电,加快了上管栅源两端电压下降。和图26相比,其桥臂串扰抑制效果基本一致,这是由于在串扰发生阶段,桥臂下管推挽电容CnL并联在下管栅源两端,因此栅源间等效并联电容为20 nF,和图26相同。
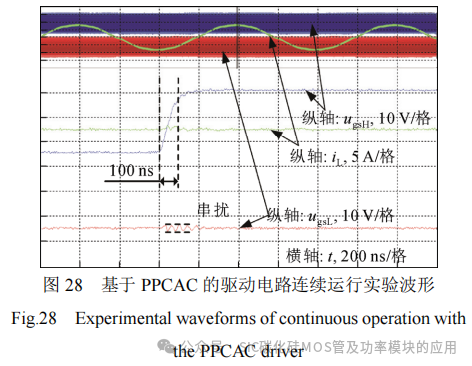
为了验证基于PPCAC的驱动电路在连续运行中的有效性,在基于SiC MOSFET的两电平变换器测试平台上进行逆变实验。直流侧接入直流电源,电压为600 V,交流侧接入三相对称阻感负载,电阻为50 Ω,电感为216 μH,输出线电压为380 V,输出频率为50 Hz,开关频率为20 kHz。实验波形如图28所示,从图中可以看出,开通时间约为100ns,与双脉冲实验结果一致,串扰电压大小约为2 V,与双脉冲实验结果一致,表明在连续运行中,基于PPCAC的驱动电路能够有效抑制桥臂串扰。
由实验结果可知,通过所提出的参数设计方法,PPCAC驱动方案可在抑制桥臂串扰的同时,提高SiC MOSFET的开关速度。由于实验条件限制,直流母线电压较低以及运行功率较小,在开关过程中漏源电压振荡不明显,本文没有进一步进行实验验证,但是栅源电压振荡的产生机理与桥臂串扰产生机理类似,由漏源电压变化通过米勒电容耦合至驱动回路,进而引起栅源电压变化,因此,PPCAC驱动在抑制桥臂串扰的同时,也可抑制栅源电压振荡。
5.结论
本文对论文作者之前所提出的基于推挽式电容辅助电路的SiC MOSFET驱动工作过程进行了进一步的分析及设计,取得以下结果:
1)将SiC MOSFET桥臂串扰以及漏源电压振荡引起的栅源电压振荡2个问题归一化,通过约束推挽电容充放电时刻以及桥臂串扰幅值,提出一种推挽电容参数设计方法。该设计可在抑制桥臂串扰与栅源电压振荡的基础上,优化SiC MOSFET开关速度。
2)通过仿真验证了推挽电容参数设计方法的有效性,并在两电平SiC变换器测试平台上进行双脉冲实验及连续运行实验,验证了基于PPCAC的驱动电路开通关断的快速性及抑制串扰的有效性。

