摘要:为增强电动汽车与电网的互动能力,车载双向充电器已成为现研究的热点。设计采用碳化硅金属氧化物半导体场效应晶体管(silicon carbide-metal oxide semiconductor filed effect transistor,SiC-MOSFET)与硅绝缘栅双极型晶体管(silicon-insulated gate bipolar transistor Si-IGBT)相结合,完成了基于双有源桥(dual active bridge,DAB)与三相四线逆变器级联的双向充电系统。通过建立逆变器数学模型分析了不平衡负载下产生分裂电容电压震荡的原因,描述了震荡幅值与负载不平衡度之间的关系,为分裂电容值的选择提供了理论依据。对实际控制系统中存在的延迟,分析使用 Si-IGBT 构建中线桥臂的可行性,提出了基于虚拟阻抗的双向充电器在不平衡负载下中线桥臂与其他 3 个桥臂之间的解耦控制方法。并使用 10kHz 与 50kHz 开关频率验证了不平衡负载下该控制方法对分裂电容电压震荡的抑制作用。提出该系统在 V2G,G2V 及 V2H 这 3 种不同工作模式下的详细控制策略,通过实验验证了不同模式下的控制策略及中线解耦控制方法的可行性和有效性。并进一步分析该拓扑结构在 V2H 模式下同时为多个不同住宅提供单相电的可能性,为采用 SiC 设计类似的电力电子设备提供系统的设计方案及控制方法。
关键词:车载双向充电器;碳化硅-金属氧化物半导体场效应晶体管(SiC-MOSFET);中线桥臂;三相四线逆变器;虚拟阻抗;控制延时
0. 引言
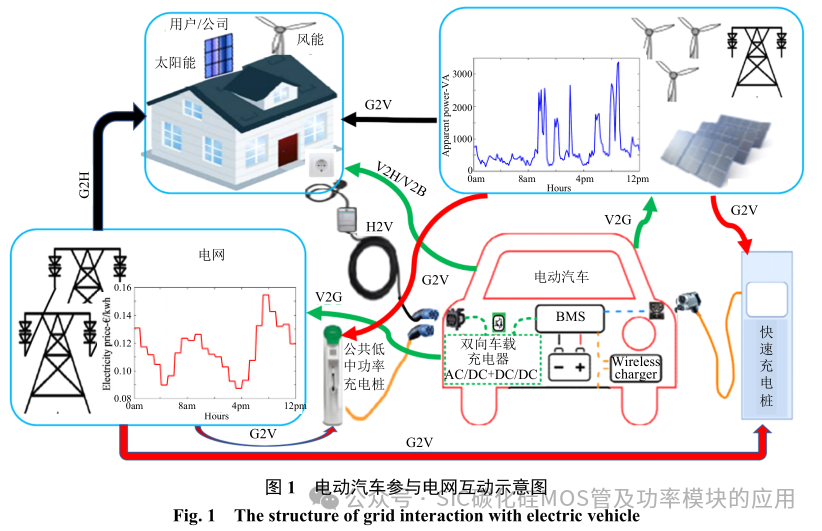
近年来,由于电动汽车数量的激增,与之配套的充电器数量也大幅度增加。目前具有固定位置的三相充电桩已广泛应用于电动汽车 (electricvehicles,EVs)。但由于充电桩位置的限制,导致充电不方便,一定程度上限制了电动汽车的发展速度。与此同时,随着近几年能源互联网在世界范围内的提出,使得以电能为载体的清洁能源得以快速发展。但由于清洁能源资源分布不均衡,导致区域供需不平衡。为解决能源的区域供需不足问题,世界范围内都在寻找一种能够使能源达到就地使用的模式,基于电动汽车的 V2H 模式正是为满足此需求而设计的一种供电形式。电动汽车的车载双向充电器在实现方便快捷充电的同时可实现V2H、grid to vehicle (G2V),vehicle to grid (V2G),vehicles to vehicles (Vs2Vs)模式,完成汽车与电网互动的功能。图 1 为具有车载双向充电器的电动汽车与电网互动的示意图。电动汽车可在公共集中式的充电站或大型快速充电站完成充电(G2V),也可以通 过 公 司 或 者 住 宅 区 直 接 完 成 充 电 (home to vehicle,H2V)充电。同时可以在用电高峰期将多余的电能直接通过集中式的并网基站实现 V2G 放电。电动汽车车载双向充电器在特殊环境(如自然灾害导致电网大面积停止工作)下,可将电动汽车电池储存的电能通过双向充电器转换直接供用户或公司使用。因此其转换效率、输出功率、功率密度、逆变后的电压/电流质量等都是车载双向充电器主要考量指标。
现有的车载双向充电器大多数功率限制在3.3kW 或 6.6kW。文献[7]中采用 900V SiC 完成6.6kW 的车载双向充电系统,在充电与放电状态效率分别可达到 96.37%与 96.87%。基于 SiC 器件的高功率密度、高效率,文献[8]提出的隔离型车载充电器在开关频率为 200kHz 时,系统的最大传输效率可达 95%、功率密度可达 5.0kW/L、重量功率密度为 3.8kW/kg。文献[9]使用 1200v SiC 与 650v GaN器件相结合的混合开关,完成了效率为 96%的三相车载双向充电器。文献[10]采用并联的 GaN 器件完成了 7.2kW 的车载充电器,达到了较高的系统效率。文献[11]使用 SiC 完成了 6.6kW 的双向车载充电器,并可在 V2G,G2V,Vs2Vs 及 V2H 等模式下工作。但从 V2G 未来的发展趋势来看,除了政府主导的通过大型充放电站实现 V2G 集中式利用的区域示范工程外,V2G 要真正变成现实必须首先使电动汽车步入家庭,V2H 是 V2G 的前奏,稳定可靠的V2H 功能是实现电动汽车安全并网的基础。
V2H 模式下,汽车需要向单相和三相混合负载供电。因此,需要一条中线为不平衡负载提供电流回路来处理不平衡负载下输出电能的质量问题。该中线回路是此类双向充电器必备的功能之一,相关中线电流控制方法鲜有报道。一般情况下对于不平衡负载时电能质量控制问题大多采用三相四线制来处理优化。文献[15]中采用分裂电容的方式提供中线电流回路,实现了三相逆变器在不平衡负载时的电能质量控制,但由于其采用硅-绝缘栅双极型晶体管(silicon-insulated gate bipolar transistor,Si-IGBT)完成,开关速率低,系统中的电容与电感值较大(母线电容:3000μF、滤波电感及电容分别为 1mH 和210μF)。文献[16]和[17]中提出中线桥臂来提供在不平衡负载下中线电流回路。此时由于中线桥臂高速的开关,中点出现高频的电压,直流端可能成为电磁干扰源影响系统的可靠性。文献[19]中只使用4 个桥臂并采用叠加的控制方法,通过输出电压的误差信号修正传输电压,在线性或非线性负载变换时保证输出电压的 THD<3%。相比于分裂电容式的三相四线拓扑结构,增加中线桥臂的一个优势在于交流电压的输出可以提高 15%,但新增的中线桥臂无法实现独立控制来获得稳定中点,相应的控制设计复杂。文献[20]与[21]中提出只采用中线桥臂作为中线电流回路,给出了相应电容电感值的选择依据及复杂的三维空间电压矢量机(3-D SVM)控制方法。其主要分析了不同负载类型及二极管作为逆变器负载时存在的问题,为不平衡负载下系统的控制奠定了基础。文献[22]与[23]同时采用分裂电容与中线桥臂作为中线电流回路的拓扑结构,其并采用不同的控制方法来减小输出电压的 THD,如:虚拟阻抗结合重复控制方法。综上可见,无论是分裂电容还是中线桥臂提供中线电流回路的方法其核心均在于系统的控制方法,控制目标是在中线桥臂的结构参数与其他 3 个桥臂完全相同的情况下配合其他 3 个桥臂来提高输出交流电的质量,现有文献未见对于能够与其他三相完全解耦且不同参数情况下进行独立控制的中线桥臂的设计与控制的报道。
本文以车载双向充电器的 V2H 工作模式为研究对象,采用双向 DC/DC 与 DC/AC 级联的方式,完成了一套车载双向充电系统。针对不平衡负载下电压质量问题,逆变部分采用分裂电容与中线桥臂相结合的方式来提供中线电流回路,并使用碳化硅–金属氧化物半导体场效应晶体管(silicon carbide-metal oxide semiconductor field effect transistor,SiC-MOSFET)与 Si-IGBT 相结合的拓扑结构降低系统整体损耗的同时降低了系统成本。针对单相和三相不平衡负载分析了采用 Si-IGBT 够成中线桥臂来处理不平衡负载以提高输出交流电质量的可行性,给出了中线桥臂与其他三相的解耦控制方法。在实验样机上实现 G2V、V2G 及 V2H 这 3 种模式下车载双向充电器的控制策略,实验验证了理论分析的正确性和控制方法在实际应用中的可行性。
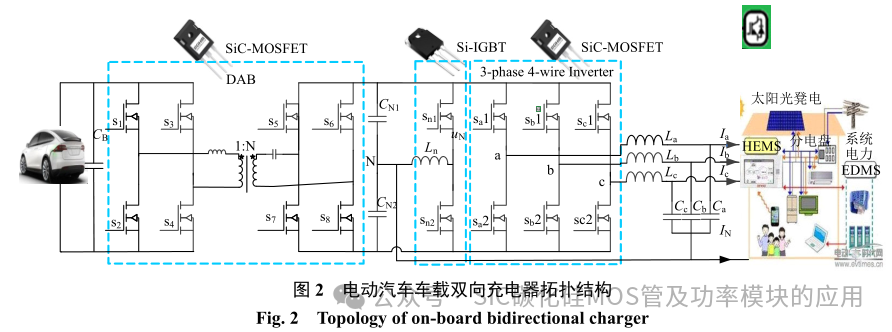
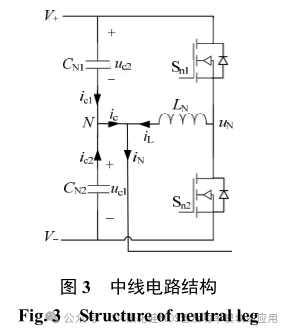
图 2 为本设计所采用的车载双向充电器拓扑结构。其主要由 2 部分构成:①双有源桥(DAB),由开关管 S1—S8 (SCT3022AL)组成,变压器一次侧与二次侧匝比设为 1:N,N 由电动汽车电池电压与三相输 出 的 交 流 电 压 决 定 。 ② 三 相 四 线 逆 变 器(3-Phase 4-Wire Inverter,3P4W-inverter) 由传统的3 个桥臂 Sa1—Sc2 (SCT3030KL)、母线分裂电容CN1,CN2 以及中线桥臂 Sn1,Sn2 构成。输出滤波采用 LC 滤波器,即:La=Lb=Lc=Lf 及 Ca=Cb=Cc=Cf,该值由系统的开关频率、输出功率、THD 等参数决定。该系统的具体参数在第 3 部分进行了详细分析。
当DAB一次侧脉宽调制 (pulse widthmodulation,PWM)控制信号的相位超前于二次侧PWM 信号时,能量由电动汽车流向用户,实现V2H、V2G 或 Vs2Vs 模式的放电功能,相应的 3P4W-inverter 采用 Sinusoidal Pulse Width Modulation(SPWM)完成控制。当一次侧 PWM 控制信号的相位滞后于二次侧 PWM 信号时,能量由电网流向电动汽车,实现 G2V 模式的充电功能。不平衡负载时中线电流的回路由分裂电容(CN1,CN2)以及中线桥臂(Sn1,Sn2)构成。DAB 部分控制采用单相移的控制方法。在放电模式下:其采用电压环控制方法实现母线电压的平稳,以确保逆变器输出稳定的三相电压,且以电流采样用于系统的过流保护。充电模式下:分别采用恒流与恒压的控制方法完成充电功能。该控制方法简单,已在文献[27]中有详细介绍。
1. 不平衡负载下中点电压震荡分析及控制
当系统工作于 V2H 模式时,其类似于微电网的孤岛运行,需要输出平稳的三相交流电。在此假设系统输出的三相电压方程为

式中:Um 为输出相电压的有效值。在实际应用中由于负载的随机性,系统可能会为单/三相或者不对称的混合负载供电。因此,每相会形成不同的交流电流,假设不平衡负载下三相不平衡电流为
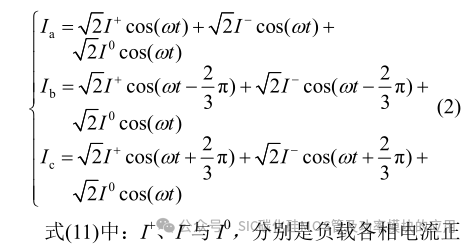
序、负序及零序的有效值。如图 2 所示结合基尔霍夫电流(KCL)定理可知:由不平衡负载引起的不平衡电流会通过中线。且当中线桥臂开关管不工作时,中线电流会使中点电压产生偏移,影响输出电压的质量。为评估不平衡负载对中点电压的影响,假设直流母线电压为

式中:Udc 为直流母线电压的直流分量; u%dc为电压上的交流分量。其交流分量越大分裂电容上电压振荡就会越大。图 3 中根据 KCL 定律可知

当三相负载平衡时 iCN=0,且分裂电容参数完全相同时,中点电压保持为定值(Vo=Udc/2),分裂电容电压交流分量 u%dc 亦为 0。当负载不平衡时分裂电容电压会随着电流的不同发生变化,假设其产生的电压波动用 △U 表示,则 △UC1=- △UC2 且与电容电流的对应关系为因此分裂电容上的电压可表示为
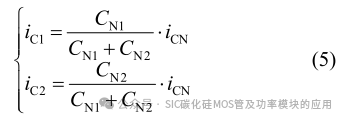
因此分裂电容上的电压可表示为
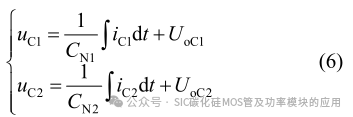
式中:UoC1 与 UoC2 均为分裂电容两端电压的直流分量。根据式(5)与式(6)电容 CN1 与 CN2 的电压振荡值为
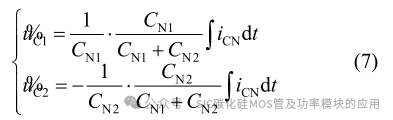
因此分裂电容电压的震荡幅值主要受中线电流的大小控制,其也影响到母线电压的震荡幅值。图 2 中根据 KCL 定律有:
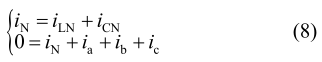
因此中线电流为
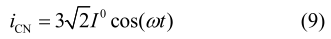
当不使能中线桥臂时,流过中线电感上的电流iLN 可认为是 0。假设分裂电容参数完全相同,则任意时刻分裂电容 CN1 与 CN2 上的电压为
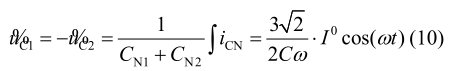
式中 CN1=CN2=C。由其可知:由于分裂电容端电压的交流成分幅值相等,且符号相反,因此直流母线总电压不会受到不平衡负载的影响。而分裂电容端的瞬时电压值会随着负载不平衡度的增大而增大,且震荡频率与输出电压的频率相同。当不平衡度增大,分裂电容端电压会大于其耐压值而损坏电容,从而导致系统故障。因此需要合理设计并控制中线桥臂以抑制分裂电容电压的震荡。
中线控制器的目标是产生互补的脉冲信号实现开关管 Sn1 和 Sn2 的开通和关断,从而使得中点电压非常接近母线电压的一半。因此可以通过保持电感 Ln 上的电流与中线电流 IN 相等来实现,即保证各电容上的电压恒定且相等。中线电路结构如图 3所示。
若所有电压均以中点 N 为参考点,则直流母线电压即中点电压平均电压可由式(1)表示。
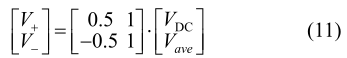
式中 VDC=V+ V-,Vave 的参考值为 0。同时根据 KCL与 KVL 可知:
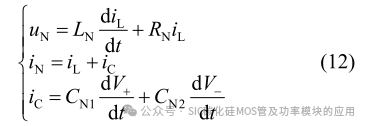
由式(11)与(12)可知:
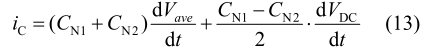
在此定义新的电压变量:
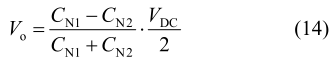
表示由于分裂电容不匹配以及 VDC 的可能变化而带来的扰动。则 ic 可表示为:
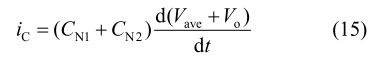
若在一个开关周期内定义
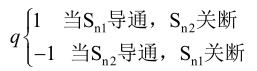
且以 p 来表示 q 的平均值,则开关管 Sn1 的占空比为:

由于中线桥臂的开关管 Sn1与 Sn2工作在高频开关下,可假设在一个开关周期内 V和 V是恒定的,则 uN 的平均值为:
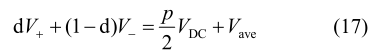
其可近似为:
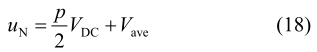
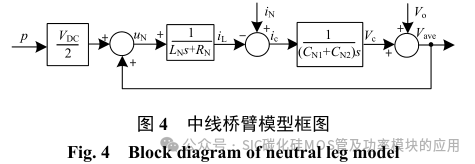
结合式(12)、(16)和(18),中线桥臂的模型框图如图 4 所示。
2. 基于虚拟阻抗的中线桥臂和三相逆变控制
2.1 三相逆变器解耦控制
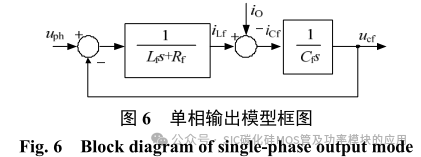
对于该三相逆变器,由于中线桥臂与分裂电容的存在,三相之间可完全解耦,每相可采用 SPWM的控制方法实现逆变。但由于输出滤波电感 Lf 与电容 Cf 亦会产生谐振,尤其使用 SiC 开关管用于高频的斩波时,系统需要的滤波电感及电容可大幅度减小,谐振频率更高。使用与电容并联的虚拟电阻以有源阻尼的方式对谐振增益进行抑制是保证三相逆变系统稳定的有效措施。因此,该系统的单相等效模型可用图 5 表示。
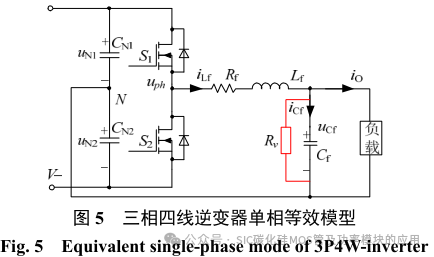
图 5 中电阻 Rv 为虚拟电阻,实际中无电流流过。因此,根据 KCL 与 KVL 可知:
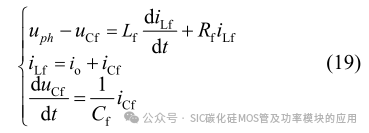
式中 uph 为单相滤波前电压,由式(19)可得其单相输出的模型框图如图 6 所示。
2.2 中线桥臂及控制器设计
为确保不平衡负载下中点 N 电压的稳定,必须合理控制中线桥臂,使大部分中线电流流过电感Ln,避免分裂电容电压发生震荡。同时当大部分中线电流不再流过分裂电容时,其电容值可以大幅度减小,进而减小系统的重量、体积及成本。由文献[17]可知:该中线桥臂等效模型类似于三相逆变器的单相等效模型,其在 LC 滤波器的谐振频率处仍然存在不稳定的可能性。因此,使用并联虚拟电阻的有源阻尼来抑制谐振频率处的增益可有效提高系统的稳定性。
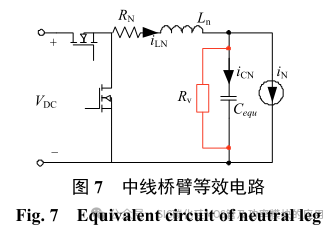
中线桥臂等效模型如图 7 所示,其中 Cequ=CN1+CN2 为等效电容,Ln 为中线电感,RN 为中线电感的串联等效内阻,其系统传输函数波特图如图 8所示。
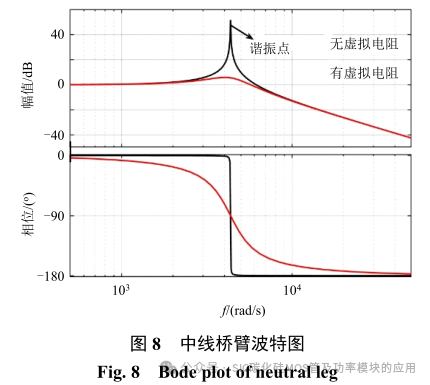
图 8 为电压控制环下的中线桥臂波特图,谐振点的增益是由中线电感 Ln 与等效电路中的等效电容 Cequ 谐振产生的。当采用虚拟负载进行抑制谐振时,可大幅度降低谐振点的增益,使系统更加稳定。为使提高中线桥臂对分裂电容电压的控制速度,提高动态响应的能力,其简单易行的方法即为加入电流控制内环。并考虑实际中数字控制系统的控制延时的情况下,中线桥臂控制框图可转换为图 9表示。
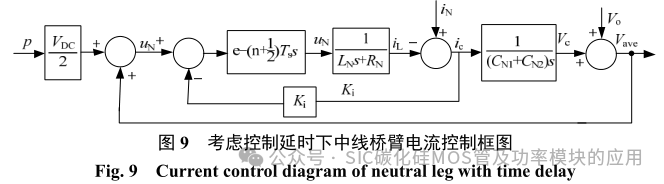
2.2.1 电流控制器 Ki 设计
图 9 中,n 是假设 PWM 信号的更新是在 n 个开关周期后、PWM 的零阶保持器延时为 0.5 个开关周期。同时如图 7 所示,由于电阻 Rv 在实际中不存在,无实际电流经过此电阻。由此,电流 iN、iCN 及 iLN 可表示为
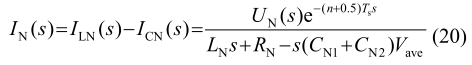
为了获取更多的电流信息,电流控制环应尽可能的需要拥有较高的带宽。由图 9 可知其开环电流传输函数如式(21)。
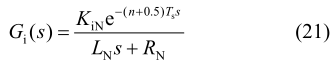
其相位角可表示为
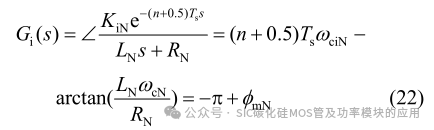
式中:ΦmN 是为保证系统稳定的最小相位裕度;RN为电感的等效内阻,由于其阻值非常小; arctan(LNωCN/RN )可近似为π/2。因此,最大的带宽为
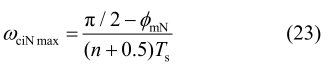
此时相对应的电流环的比例控制参数可表示为下式(24)。
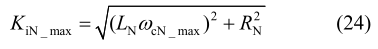
2.2.2 电压控制器比例系数 Kv 的设计
电压控制器的目的最大可能的抑制中点电压的偏移。由此,需要以获取最大的电压控制环带宽为目的设计响应的电压控制参数。当以电压为控制量时,图 4 可简化为图 10 所示,其传输函数为
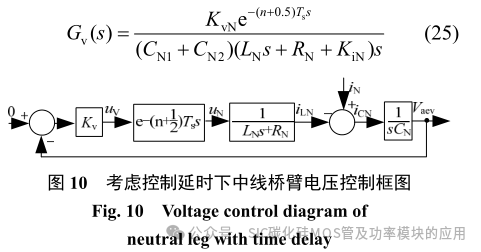
为增强电流内环对电压控制的效果,内环的带宽通常设计为外环的 5 倍以上。本设计中电压外环的带宽设计为内环的 1/10,即:
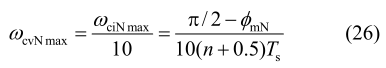
根据式(21)—(25)同理可知电压控制参数可表示为
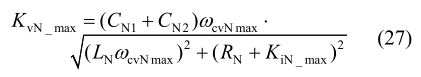
如上面分析可知:为使系统达到预期的传输效率,逆变器最大开关频率定义为 50kHz。当降低开关频率时,可有效降低开关损耗提高系统传输效率。基于此分析,本设计采用较低的频率开关速度来控制中线桥臂。而其他三相保持 50kHz 不变,以保证相同的 LC 滤波参数而不增大系统体积的同时实现较低的输出电压纹波。但由于数字控制系统中控制延时的存在,必须针对不同的控制延迟验证在此低频下系统的稳定性。因此在此假设中线桥臂开关速度为 10kHz,结合虚拟电阻,中线桥臂控制系统在不同控制延迟 n 时波特图如图 11 所示。
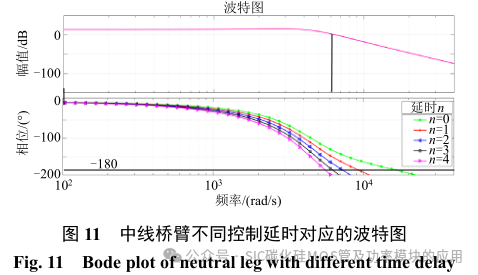
图 11 所示:当控制延时 n≥3 时其穿越频率接近于 180°,系统处于不稳定状态。当 n=2 时,相位裕度较小(<20°),系统亦容易失去控制。而在 N=1时,相位裕度约为 30°,其可以保证系统安全稳定的运行。控制频率在 10kHz 时,其数字控制延迟可保证在 1.5 拍内,即:可保证 n≤1。因此,当中线桥臂工作频率为 10kHz 时,可稳定有效地完成对中点电压的控制。
3. 系统参数确定及仿真分析
为使系统在 20kVA 容量下能达到 97%的效率,本设计首先对 2 种 SiC 开关管进行了双脉冲测试,门级电阻分别取 2.7Ω与 2Ω,驱动回路采用 4 层PCB(Print Circuit Board)完成。所得开通与关断时的损耗曲线及相应的拟合曲线函数如图 12 所示。根据数据手册所提供的信息,本系统中的 SiC 开关管均采用+20V 开通、-4V 关断,此时可减小系统损耗。
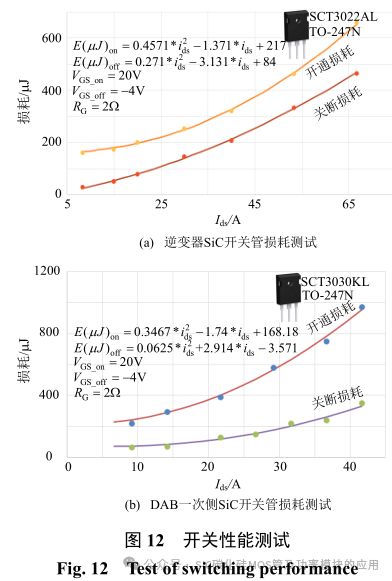
由图 12 可知,开关管的开通损耗远大于关断损耗,由于 DAB 侧通过控制算法容易实现 ZVS(zero voltage switching)技术,但三相逆变器侧则始终工作于硬开关状态。因此,可在保证门级驱动回路安全的情况下可适当减小逆变器侧的开通时间来提高系统的整体效率。对于 DAB 与逆变器开关管分别采用 2.7Ω与 2Ω不同的门级电阻。最终由MATLAB 拟合的各部分损耗函数式如式(28)—(33)。
DAB 部分(原边+副边):
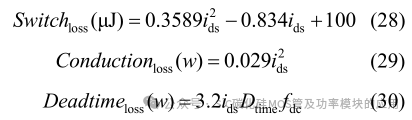
逆变器侧:
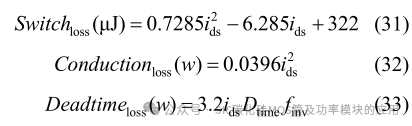
式(26)与(29)中,导通损耗电阻值均来源于该器件厂家所提供的数据手册,相应的式(27)与(30)中死区损耗由死区时间、SiC 体内二极管的导通压降(由数据手册提供)、该时刻流过的电流及开关频率决定。该系统最终 DAB 部分开关频率定为 100kHz,三相逆变部分开关频率则定为 50kHz。
当系统处于极端不平衡(某相处于开路)状态时,中线桥臂开关管流过的最大电流为 56A。因此,本设计选用的 IGBT 为 NGTB40N120IHRWG。由文献[29]可知:中线电感可根据式(34)选取。
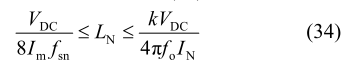
式中电流 Im 与 IN 分别为开关管最大允许的电流和中线电流;VDC 为直流母线电压;fsn 与 fo 分别为中线桥臂开关频率与三相交流电输出频率;k 为 0.8~1的系数,其取决于 PWM 波形的产生机制。三相输出端 LC 滤波器参数根据文献[32]得出,该系统详细参数如表 1 所示。

根据表 1 所示系统参数,在加入电流环时不同开关频率下中点电压偏移控制效果仿真如图 13 所示。
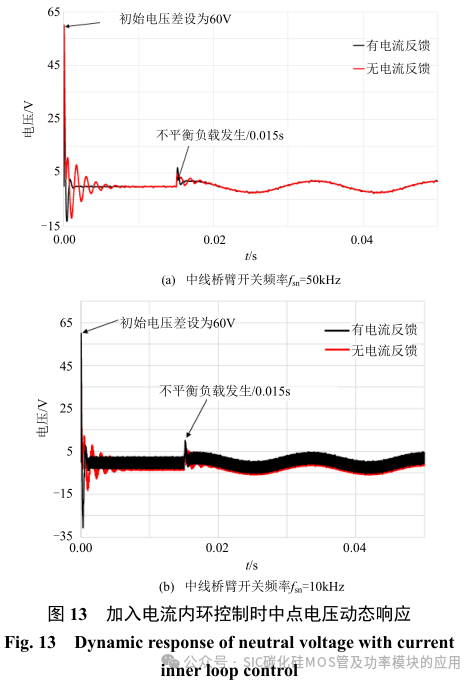
图 13 显示了不同中线桥臂开关频率下中点电压调节的动态过程。在设置初始电压偏移为 60v 时,无论开关速度采用 50kHz 或 10kHz,中点电压偏移都可以调节至 0V 附近。当不平衡负载发生时,50kHz 和 10kHz 的开关速度均可调节中点偏移电压至 5V 以下。且由图可知:无论是初始较大的电压偏差或是不平衡负载发生时,在加入电流反馈时的控制器均有较快的调节能力。当不平衡负载存在时,三相四线逆变系统各部分仿真波形如图 14 与图 15 所示。
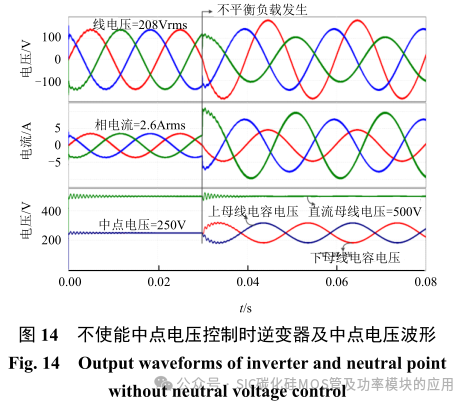
由图 14 可知:当不平衡负载发生如不使能中点电压控制时,中点电压会有较大的偏移。其跟随着逆变器输出的交流电压同频率的出现震荡。且此震荡幅值将随着不平衡负载的增大而增大,即:iN越大,中点电压震荡幅值越大。其与式(10)所分析的结果相符合。
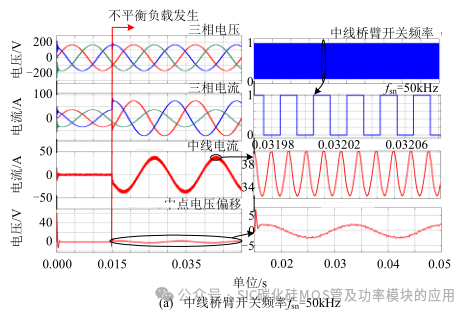
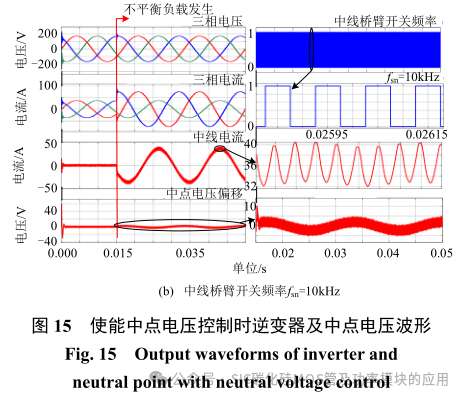
由图 15 可知:当不平衡负载发生时使能中点电压控制,且以不同开关频率使能中线桥臂时,中点震荡电压幅值均能被大幅度的减小。图(a)与(b)中分别采用 50kHz 与 10kHz 控制相同的中线电流 iN 时,中点震荡电压幅值均能被控制在5V 以内。而仅有的区别在于低频 10kHz 时,中点电压的纹波较大。但其不会影响三相交流电压的输出质量,更不会影响分裂电容耐压值的选取。
如引言中所述:在 V2H 模式下电动汽车会向单相和三相负载混合供电,在此假设某时刻该双向充电器同时向 3 个不同的用户供电,且负载大小可随时发生变化。当中线桥臂开关频率为 10kHz 时,其仿真结果如图 16 所示。
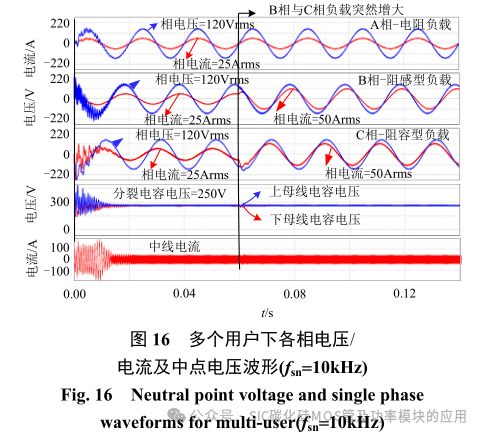
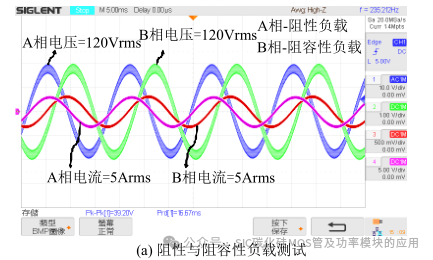
如图 16 中所示为该三相四线逆变器在完全解耦的情况下,由 SPWM 控制输出 3 个独立的单相交流电供 3 个用户使用。假设该 3 个户用负载类型各不相同(A 相负载为纯阻性,B 相负载为阻感性,C 相负载为阻容性),此时直流母线电压为 500V。在 0 至 0.06s 内各相负载电流大小相等(有效值为25A),三相输出电压稳定,分裂电容端电压相等。在 0.06s 时刻,B 相与 C 相负载突然增大,由图可知 3 个独立的单相电压发生波动后可很快的恢复正常,母线分裂电压短时间内有所震荡,在经过 0.01s后中点电压恢复至母线电压的一半(250V),分裂电容的端电压在本文所提出的控制策略下仍保持不变。因此,采用价格更便宜的 Si-IGBT 构建该系统的中线桥臂,并以用较低频的开关速度控制管子的开通与关断,亦可保证系统适用于不同的应用场合。与此同时此结构设计不仅可以降低系统的成本,而且可以在不改变系统其他参数的情况下,能降低开关损耗来提高整体系统的工作效率。
4. G2V、V2G、V2H 模式控制原理及实验分析
根据以上分析,本文完成三相四线车载双向充电系统一套,该车载系统可工作在 G2V、V2G 及V2H 这 3 种不同模式下。实验测试中,模式的切换由上位机通过 CAN 通信接口向处理器发送指令完成, 各部分的控制由独立的 DSP(Digital Signal Processing)处理器完成。因此,总系统由双控制器(DSP: TMS320F28335)完成,不同模式下的详细控制策略由及相应的控制指令如图 17 所示。
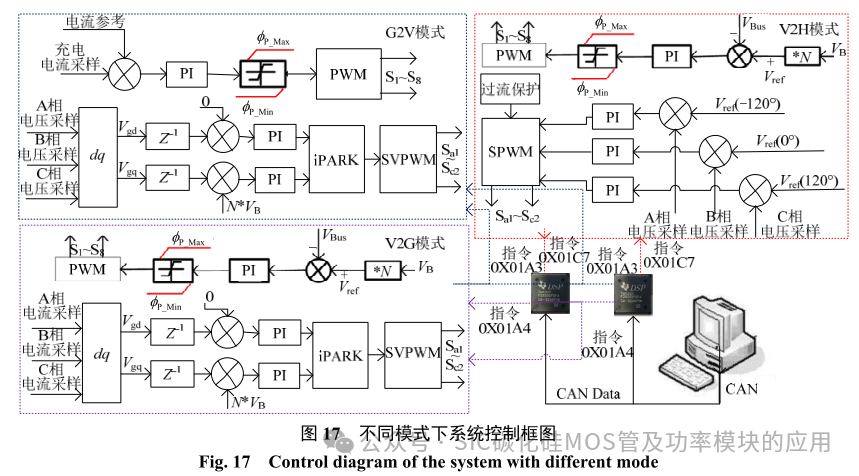
图中ΦP_Max 与ΦP_Min 为 DAB 侧进行移相控制中相移的最大值与最小值,用来控制最大输出功率。VB 为电池电压,电流的采样用来实现系统的过流保护。由于在 G2V 与 V2G 模式下中线桥臂均不需要,因此在实际应用中通过继电器将其与其他三相断开。而在 V2H 模式下使能中线桥臂来消除因不平衡负载引起的分裂电容电压震荡的问题。根据以上分析与设计,该系统功率板布局及形成的样机如图 18 所示。由图可知其有很大的空间未被有效利用,主要原因是由于该系统最初的测试目是验证该拓扑结构在 V2H 模式下不平负载时的可靠性和采用 SiC-MOSFET 形成的系统传输效率,而对整体系统的机械降温结构没有做特有的设计,因此其功率密度较低。整体系统最终采用水冷系统完成对样机的降温。

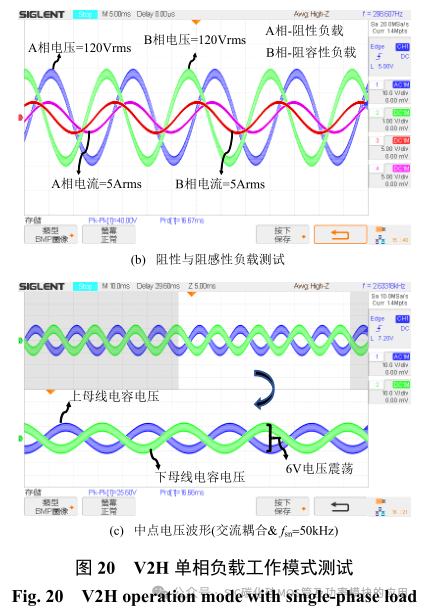
V2H 模式是该系统的主要研究对象,其类似于三相逆变器的孤岛运行,保证三相交流输出电压的平稳是主要目标。因此在汽车电池向负载释放能量时,本系统的 DAB 侧以电压环作为控制器,保证直流母线电压的平稳。其采用单相移控制策略将电池电压进行升压,并在三相四线逆变器侧经过三相解耦的 SPWM 控制技术进行三相逆变以供负载使用。不同于其他两种模式,该模式下使能中线桥臂以避免不平衡负载下中线电流对系统的影响。如图 19 所示为 V2H 模式下的测试平台及波形。在此过程中高压直流电源用来模拟汽车电池,以交流照明灯与大功率电阻作为交流负载。
如图 19(a)所示为 10kW 阻性平衡负载下 DAB与逆变器部分的主要波形,此时 DAB 部分开关管均工作在零电压开通(ZVS-ON)状态。图 19(b)、(c)分别为阻性不平衡负载下不使能与使能中线控制时逆 变 器 输出及 分裂电容电压波形 ( 其中fdc=100kHz,finv=50kHz,fsn=50kHz)。负载平衡且稳态运行时,每相负载为 47Ω电阻,在某个时刻通过手动开关在一相上并联相同的电阻(如图 19(e)所示)。因此并联电阻的电流增大(由 2.6Arms 增大至 4.4Arms),而在不使能中线桥臂时,零序列电流则通过中线进入分裂电容。因此分裂电容电压会产生与输出电压同频率的震荡,同时三相输出电压也产生了不对称,如图 19(b)中其中一相电压幅值高于其他两相。
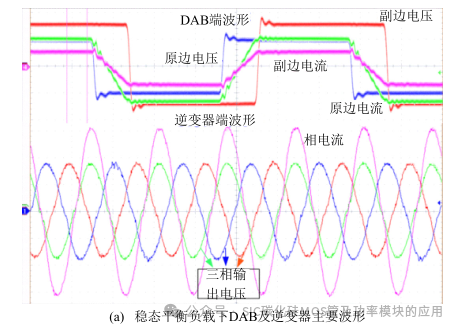
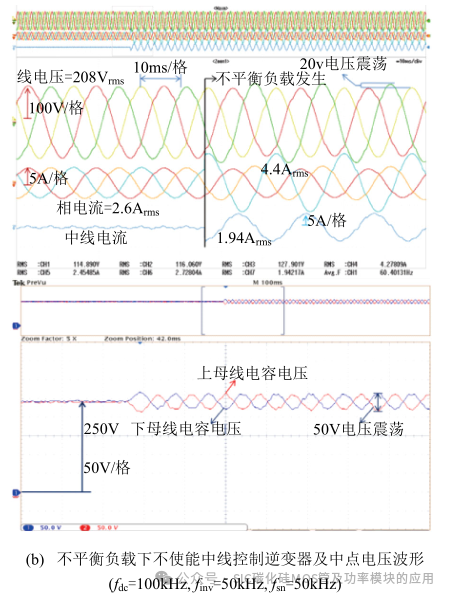
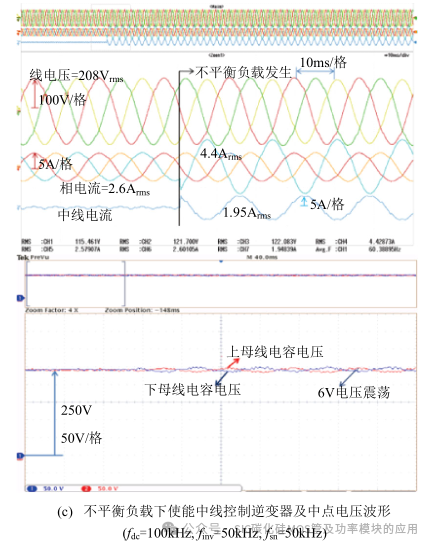
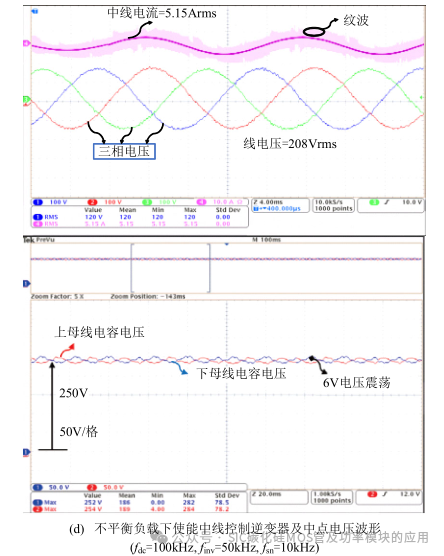


图 19(c)相比于图 19(b),其三相逆变器输出电压波形即使在不平衡负载发生时仍能保证对称的三相交流电,且分裂电容电压的震荡幅值由 50V 减小至6V。因此可知:通过对中线桥臂的控制,在不平衡负载发生时,大部分的中线电流流过中线电感,从而减小了分裂电容的电压震荡。为验证中线桥臂在不同开关频率下对分裂电容电压震荡的抑制情况,
图19(d)显示了当fdc=100kHz, finv=50kHz, fsn=10kHz时三相输出电压及分裂电容电压震荡的问题。其与仿真结果相似,相比于 50kHz 中线开关频率电压电流的纹波增大,叠加在分裂电容上的电压基波有效值未增大,因此进一步证明了采用 Si-IGBT 构建中线桥臂的可行性。图 19(e)、(f)分别为 V2H 模式下不平衡负载与稳态平衡负载下的测试平台。
由图 16 仿真分析可知:该三相四线逆变系统可为单相或三相负载供电,因此在输出的三相交流电中分别加纯阻性、阻容性及阻感性负载至 A 相、B 相及 C 相,其电压电流波形如图 20 所示。其中阻感性负载由 500uH 的电感与电阻串联构成,在阻容性负载由 470uF 电解电容与电阻并联构成。此时在本文所设计的中点电压控制方法下,中点电压的波形如图(c)所示。其中点电压的震荡幅值与图 19(c)中基本保持一致,验证了该双向充电系统为单相与三相负载供电的可行性,验证了之前的理论与仿真分析。
本文主要研究 V2H 模式下三相四线逆变器及其中线桥臂的设计及控制,为说明该拓扑结构在G2V 与 V2G 模式下的可行性,实验测试如下。
G2V 模式下 DAB 模块采用电流与电压的双控制策略完成对电池的三段式充电。此时双向三相四线逆变器中中线桥臂不使能,剩余 3 个桥臂采用传统 SVPWM 实现整流及功率因数的校正。如图 21所示为 G2V 与 V2G 模式下的主要电压与电流波形,在 G2V 模式下其功率因数约为 0.956,而对于其性能的进一步优化在众多文章中已有深入的分析,在此不做说明。
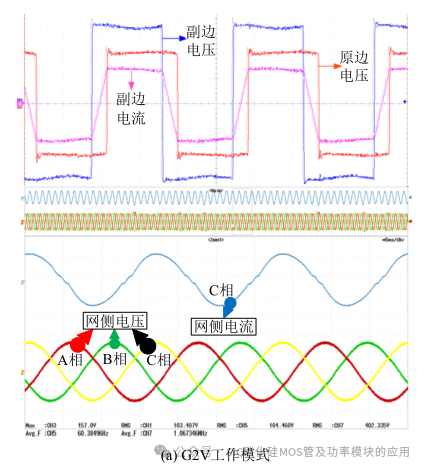
如图 17 所示,当上位机通过 CAN 总线向两个处理器同时发送 0X01A3 时,处理器会使 DAB 与三相逆变器工作在 G2V 模式下。此时 DAB 原边侧电压相位超前于副边侧电压,相位超前越大充电功率越大。如图 21(a)所示为恒流模式下充电电流为10.56A 时的电压与电流波形。此时充电对象用电子负载来模拟,三相输入直接由电网提供。
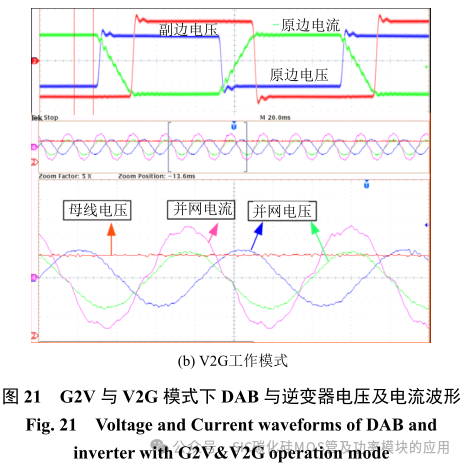
V2G 模式是将电动汽车电能通过该双向充电器注入电网,其多数是在用电高峰期电网压力大时使用。DAB 模块的工作原理与 V2H 模式下工作原理相同,采用单相移控方式与电压环的控制方式完成。逆变器侧则不使能中线桥臂,采用 SVPWM 完成并网功能。如图 20(b)所示为 V2G 模式下的主要波形此测试平台,逆变器输出端直接与 208V 电网相连。由图可知并网电压与电流为同相位,且直流母线电压平稳。
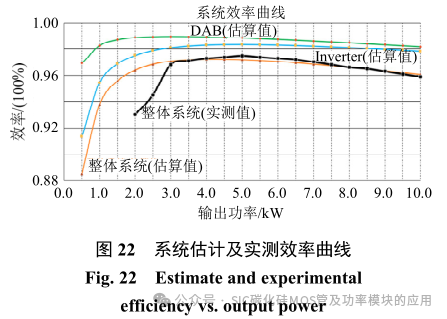
最终通过多个电压与电流表对实际工作效率的测试曲线如图 22 所示,其中估算效率由式(28)—(33)根据文献[33]获得。因为母线电压较高,在轻载情况下 DAB 端电流较小,采用单相移控制策略的 DAB 部分容易造成软开关失败,因此在开始时,实测效率曲线低于估计的效率曲线。对于类似的级联系统,要是进一步提高系统传输效率,在DAB 部分可采用多相移控制方法,实现全功率范围内的软开关,可再次提高系统效率。此时系统中最大传输效率可达 97.5%。
5. 结论
参与电网互动作为电动汽车一个新的扩展应用领域,本文首先分析了车载双向充电器的发展需求,给出建立三相四线逆变器来满足不平衡负载应用时的必要性。并采用双有源桥与三相四线逆变器相级联的方式形成车载双向充电系统一套,给出了通过分裂电容与中线桥臂为不平衡负载下的中线电流提供回路的优势。
本文主要针对 V2H 模式中不平衡负载下中线电流对母线分裂电容的影响,分析了中线电流对分裂电容端电压影响的根本原因,并给出了负载不平衡度与分裂电容容值及瞬时端电压之间的关系,为分裂电容容值的选择提供了理论依据。通过分析可知:分裂电容端电压主要受中线电流基波最大值的影响,本文提出了采用 Si-IGBT(中线桥臂)与 SiC-MOSFET(其他三相桥臂)混合开关管构成系统的方案,并给出了与其他三相完全解耦的中线控制方法及控制器设计过程,通过对不平衡的三相及相互独立的单相负载放电测试,验证了该系统在不同应用场合(单相或三相)下的适用性。同时该混合开关组合方式可在保证系统其他硬件参数不变的情况下,可有效降低系统成本,提高系统的传输效率。
其次,本文通过双脉冲测试给出了精确的开关损耗拟合函数式,以估计系统的传输效率。最终,针对该系统结构给出了 G2V、V2G 及 V2H 这 3 种不同模式下的工作原理及其相应的控制策略,并对不同的工作模式分别进行实验测试,验证了双向充电系统在实际应用中的可行性。经过测试该系统传输效率达到 97.5%,为采用 SiC 设计类似的电力电子设备提供了系统的设计方案及优化方法。

