文章来源：哈尔滨工业大学-丁四宝
摘要：随着第三代电力电子功率器件的商业化，以碳化硅(SiC)为代表的宽禁带半导体以其卓越的性能推动着电力电子技术的进步。受到现有生产工艺的限制，中高压大功率等级下，器件的串并联成为一种经济有效的扩容方式，然而寄生参数对于 SiC 器件串并联结构的均流均压特性的影响是亟待解决的问题。本文以SiC 功率器件作为研究对象，在串并联提升功率等级的应用背景下，研究 SiCMOSFET 的并联均流特性及串联驱动电路结构。
本文首先对现有的并联均流方式进行简要论述，为进一步研究 SiC 器件的并联均流特性，建立计及寄生参数的 SiC MOSFET 等效模型，量化分析具体的开通关断过程，给出各阶段 SiC MOSFET 的栅源极电压和漏源极电流数学模型。结合数学模型给出并联 SiC MOSFET 动态均流和静态均流临界条件，在此基础上分析了寄生参数差异在动态均流和静态均流中对均流效果的影响。
基于 SiC MOSFET 的并联硬件实验平台对上述影响均流差异的参数进行验证性实验，确定均流过程中的主要影响参数及其影响关系，为并联方案设计提供有效依据。
其次针对 SiC MOSFET 的导通电阻具有正温度特性的特点，研究了 SiC 器件损耗、温度和并联均流之间的耦合关系。结合参数模型和 SiC MOSFET 的开通、关断模型，对 SiC MOSFET 的器件损耗进行了推导，进一步采用离散化损耗–温度方程的方式，分析损耗提升结温对并联均流的影响趋势，在 PLECS 软件中验证了理论分析的正确性。
最后，为了解决串联 SiC MOSFET 采用单个电源进行驱动时，传统有源钳位驱动结构会造成串联 SiC MOSFET 存在到驱动电压延迟进而造成动态不均压的问题，本文提出一种基于多绕组变压器的隔离型串联驱动结构，并分析了其工作原理、工作模态和提出相关器件设计方案，搭建了仿真模型对驱动方案进行验证。所提驱动结构既有效保证了控制侧和功率侧的电气隔离，又能实现串联 SiC 器件的驱动电压同步性和串联 SiC MOSFET 的动态均压。
关键词：SiC MOSFET；动态均流；静态均流；损耗分析；串联驱动
Sic功率器件的介绍
碳化硅(SiC)和氮化镓( GaN)等半导体材料器件以其优异的器件性能开始替代传统 Si 半导体材料，开始用于制备电力电子功率器件，宽禁带半导体功率器件经过多年的发展逐步成熟并开始商业化应用。
宽禁带半导体主要指器件得能禁带宽度大于 2.2eV 的半导体器件，SiC 材料作为宽禁带半导体的代表，备受青睐，利用其优良的结构特性，使 SiC 功率器件在高压高温等 Si 功率器件难以胜任的复杂极端应用场合中大放异彩，解决由于器件特性导致的诸多问题，简化现有设备结构同时提升效率。硅元素和碳元素都为 IVA 族的类金属元素，原子特性决定了 SiC 的晶体单元结构是四颗碳原子和一颗硅原子构成SP3 的锥形四面体结构，从而保证了 SiC 材料具有稳定的特性。SiC 单元堆叠方式，也构成了不同的 SiC 材料不同的同质异形体的晶体形态，其中最常见的 SiC 晶体结构有 3C-SiC、4H-SiC 和 6H-SiC 三种。三种 SiC 晶体和 Si 材料的特性对比如表 1-1所示。通过表中的数据，可以明显发现 SiC 材料相比于 Si 材料在能禁带宽度、导热率、临界击穿场强和电子饱和速度等方面具有明显优势。
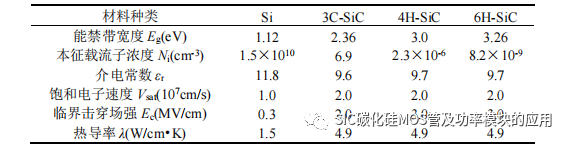表 1-1 Si 与 SiC 材料特性参数比较
根据上面表格中Si 和SiC 的材料特性参数对比，如图1-1 所示，为SiC 器件和Si 器件的性能比较，可以直观地看出相比于Si 器件，宽禁带半导体SiC 功率器件具有下优势：
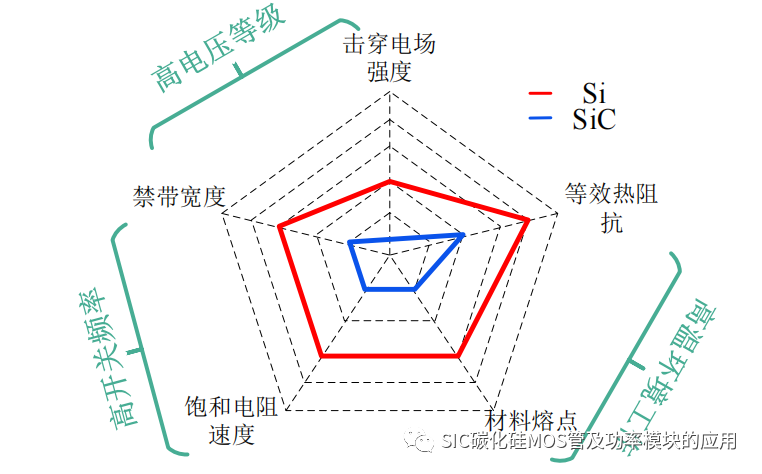
图 1-1 Si 和 SiC 器件特性比对
(1) 更宽禁带宽度：更宽的禁带宽度，确保了 SiC 器件的承受温度更高而晶体结构依然保持稳定；此外 SiC 具有更高的热导率，意味着 SiC 的器件晶圆与外壳之间的等效热阻更低。相比于 Si IGBT 手册中的 150℃耐受温度，SiC MOSFET 最大承受温度可以达到 300℃。更高的耐受温度和更低等效热阻，将有效降低 SiC器件所需的散热器的体积，同时 SiC 器件可以用在更高温度的环境中。
(2) 更低的载流子浓度：宽禁带半导体 SiC 的本证载流子浓度相比于 Si 的更低，保证了的 SiC 的漏电流更低。漏电流的越小，功率器件关断状态下的阻断效果越好，可以承受更高的电压，此外当关断漏电过大时，关断状态下的关断损耗将会提升，而不可乎略，系统效率将会降低。
(3) 更高饱和电子速率：由于 SiC 器件的高饱和电子速率特性，相同电流等级下达到饱和电流所需的时间更短，开通关断过程持续的时间更短，SiC 器件可以工作于更高的开关频率下，相比较于 Si 功率器件，更高的开关频率，可以有效的减小滤波电路的体积，节约成本，提升电力电子功率电路功率密度。
(4) 更高临界击穿场强：SiC 器件的击穿电压比Si 功率器件的高十倍，在相同电压功率等级下，SiC 器件的晶圆更小更薄，这样可以有效地降低 SiC 器件的导通电阻，在导通过程中的，应用 SiC 器件的电路导通损耗更小，作为电力电子器件损耗的主要组成成分，降低导通损耗可以有效地提升电路效率。此外更高的击穿电压，可以将 SiC 器件应用到高压大功率场合，减小串联并联所需要的器件个数，提升电路整体的可靠性。
SiC 器件代替Si 功率器件应用于电力电子电路中，能够有效的提升电路系统的性能主要有以下原因：首先 SiC 的导通电阻更小，开通关断时间更短，因此显著地降低了电力电子器件应用时引起的导通损耗和开关损耗，提升系统整体效率；其次SiC 器件的更高的耐受电压，可以提升电路容量，尤其在中高压电力系统和柔性直流输电系统中，对于器件的电压等级都有严格的要求；最后由于 SiC 器件的更高开关频率可以减小滤波电感电容的体积，更高的耐受温度，无需 Si 器件系统中的大功率散热器，这对降低电力电子设备的体积具有深远影响，尤其在汽车驱动等方面。
SiC 功率器件研究现状及应用
现代电力电子功率器件的发展时间轴如图 1-2 所示。
SiC MOSFET 的优良性能，决定了其应用领域的广泛，主要有电动汽车、新能源输配电设备和电子信息通讯等领域。从2013 年SiC 器件开始普及后，SiC 器件在的风电、光伏、新能源汽车及工业控制、通信领域的应用规模逐年递增。SiC MOSFET 提升系统效率及设备体积，广泛应用于光伏逆变器中；在电力设备领域，CREE 公司和 GE 公司制作的 10kV 系列和 13.8kV 系列固态继电器，体积减小约 40%。在电机驱动领域，采用SiC 器件制作的电机牵引设备可以有效减小 66%的占用面积，同时减小 70%的能量损耗；在电动汽车领域，安森美发布了更稳定、承受电流更高、开关速度更快的汽车级 SiC 二极管；CREE 和 ST 公司签署 150mm SiC 晶圆的供货协议，后者将生产汽车级 SiC 功率器件，此外 CREE和德国大众公司合作开展相关电动汽车驱动等相关领域的研究，特斯拉公司在去年搭建了一台基于 ST 公司的 300KW SiC 逆变器。随着 SiC 功率器件的工艺的发展，SiC MOSFET 将会在更多领域物尽其用。
SiC MOSFET 并联均流技术研究现状
虽然SiC 器件相比于Si 器件的电压电流容量更大，但是受到现有 SiC 芯片技术的限制，大容量的SiC 模块成本高，所以采用相同电压等级的SiC 单管器件进行串并联使用，来满足所需的电压电流等级成为一种经济有效的方式。但是由于 SiC MOSFET 个体之间存在寄生参数不一致，会影响 SiC MOSFET 并联应用性能，导致并联的器件支路电流存在差异，进而造成系统的性能受到影响。虽然SiC MOSFET 的出现时间不短，但相关的研究不如 Si 功率器件，因此Si IGBT 的相关并联均流方式研究相比较下更完善。
SiC MOSFET 并联均流研究现状
SiC MOSFET 的相关并联研究主要集中于对影响SiC MOSFET 的并联均流差异的因素进行测试和分析。由于SiC MOSFET 的器件特性比 Si IGBT 更好，工作频率更高，开通关断的时间更短，因此上述针对 IGBT 并联结构并不完全适用于更高工作频率下的 SiC MOSFET。而串联阻抗法对于本身导通电阻仅毫欧级别的 SiCMOSFET 效果较好，但是在大功率场合下，需要并联的 SiC MOSFET 器件个数较多，串联过多的阻抗，将会引起更高的导通损耗，违背了应用 SiC MOSFET 以提升电路效率的本意。
目前针对SiC MOSFET 的并联均流研究主要有：通过建立 SiCMOSFET 的数学模型和实验的方式研究了 SiC MOSFET 的器件和电路参数不一致对并联均流的影响，但是文章所建立的模型并没有将 SiC MOSFET 的动态均流过程和静态均流过程分开考虑；通过有限元模型分析了并联电流不均衡导致的功率分配对的温度不平衡的影响，进一步分析了模块连接器之间的电热特性对模块运行的鲁棒性的影响，进一步量化分析驱动电阻、损耗和的结温之间的度量函数，表明 SiC 的并联热特性具有更好的弹性，SiC 模块展现出更稳定的开关损耗特性和输出特性；通过开通关断瞬间的峰值电流进行建模分析，确定了影响峰值电流的因素，并进一步提出一种利用耦合电感的连接方式，可以促进 SiC MOSFET的并联峰值电流平衡，然而文献仅是针对动态均流进行相关研究，并未涉及静态均流阶段；另一种如图 1-3 所示的，串联反向耦合电感的方式实现并联的动静态均流，利用耦合电感的磁场抑制不均衡电流增长，然而由于 SiC MOSFET 的关断时间很短，将会通过接入的耦合电感产生较大的关断过电压，对于高电压容量下的 SiC MOSFET 器件可能造成损坏。
尽管上述所提的方法可以实现 SiC 器件的并联均流，但是引入外接的补偿电路，或者加入耦合电感的方式来限制不均衡电流的增长，都需要接入额外的功率器件，既增加了电路的体积，也将原本的电路复杂化，因此研究影响并联 SiC 器件均流的因素，并通过消除影响均流效果的因素和实现自身并联支路的一致性保证均流，不仅保证了稳定性，而且降低了外接器件的损耗，提升了电路的整体效率和功率等级，是一种最高效的并联方式。
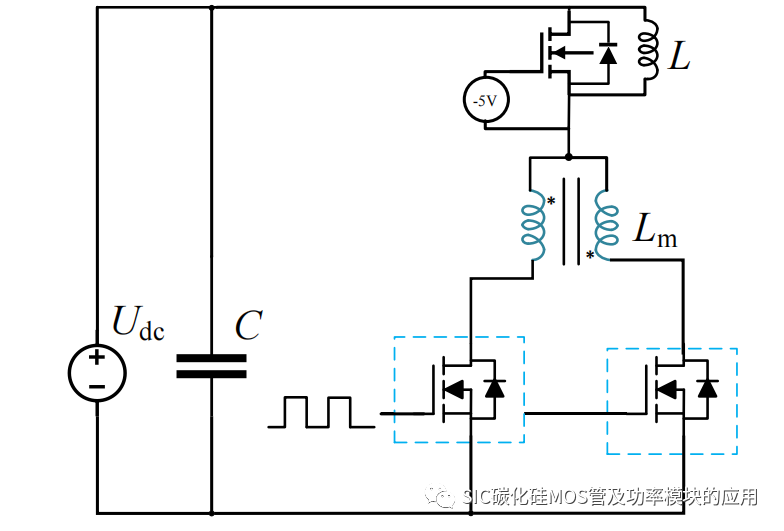
图 1-3 基于耦合电感的并联均流方式
SiC MOSFET 串联研究现状
与并联SiC MOSFET 的电流容量进行扩展的目的相同，在中高压电压等级下，SiC MOSFET 单管的耐受电压等级不足时，可以依靠串联的连接方式使 SiC MOSFET 满足电压等级需求。
SiC MOSFET 串联均压研究现状
IGBT 的负载侧串联均压结构，需要外接缓冲电路来实现，会在泄放回路电阻造成较大的能量浪费，此外加缓冲电容后，对电容的充电时间将会限制SiC MOSFET的导通关断时间，影响SiC MOSFET 工作频率。因此更多的SiC MOSFET 采用栅极有源钳位控制均压的方式，该方式只需要采用一个驱动信号来控制全部串联的 SiC MOSFET，可以保证同步性。
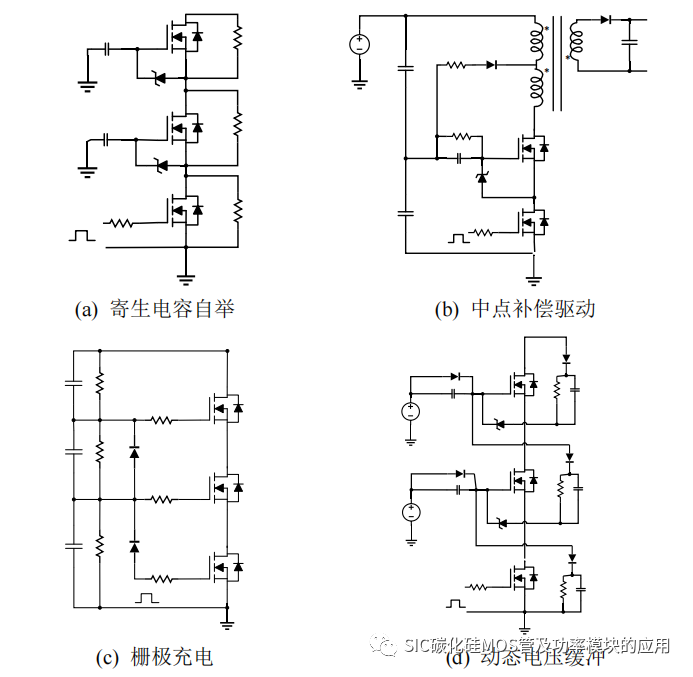
图 1-4 栅极有源钳位驱动均压串联结构
如图 1-4所示，SiC MOSFET 栅极有源钳位驱动串联均压结构，该串联均匀驱动的核心结构是充分利用电容的电荷变化来实现除连接驱动电路外的串联 SiC MOSFET 器件驱动信号转变。此类串联结构可以视为驱动控制条件下的主/从控制。每一个所属控制信号之间会存在时间延迟。图1-4(a)所示为提出的一种利用 SiC MOSFET 寄生电容充电方式实现串联驱动信号同步；如图 1-4(b)所示提出一种基于变压器中点补偿的串联驱动结，主要应用于高频开关电源中，可以较好的实现串联电压均衡；提出一种基于RC 平衡网路的，通过对串联 SiC MOSFET 的栅极之间串联的充电电阻在的开通中进行充电，关断过程放电实现 SiC MOSFET 的依次关断，提出串联单驱动结构如图 1-4(c)所示；如图 1-4(d)所示的利用 RCD 钳位和缓冲电容的形式单驱动串联均压结构，依靠下管的导通拉低与之串联的上管的源极等效电势后，驱动电源对栅极电源的进行充电，串联 SiC MOSFET 逐一导通。上述有源钳位串联驱动方式，都仅需要为串联的支路中的一个 SiC MOSFET 提供驱动电源即可，即可实现 SiC MOSFET 的依次开通和关断，然而在导通过程中，串联的 SiC MOSFET 存在导通顺序，导通顺序越靠后的 SiC MOSFET 将会承受越高的断态电压，会限制了此类方案的应用场合；而且串联 SiC MOSFET 的逐个导通的方式将会加大导通时间，当串联 SiC MOSFET 数量较多时，会限制串联 SiCMOSFET 组的工作频率；此外串联 SiC MOSFET 的连接方式决定上管的驱动源极和下关的漏极相连，对于使用相关钳位二极管、电压、电阻的耐压和绝缘强度有了更高的要求，将会增加应用的大功率电路的整体体积。
综上所述，研究SiC MOSFET 串联结构下单一驱动电路，实现串联SiC MOSFET驱动信号的同步性和开通关断的一致性将既有效保留了 SiC MOSFET 高频优势，又以一种低经济手段达到提升耐压等级的目的。
SiC MOSFET 的基本结构和工作原理
SiC MOSFET 作为一种新兴被推广的宽禁带半导体器件，尽管 SiC MOSFET相比于传统的 Si 基功率器件具有更高临界击穿电压、更耐受温度、更高工作频率和更高的载流子浓度等优势，但其工作原理和传统的 Si 基 MOSFET 仍是一致的。如图 2-1 所示，为垂直导电型的 SiC n-MOSFET 器件的元胞单元结构示意图，相比 Si MOSFET，SiC MOSFET 是以 SiC 材料作为衬底单元的，相同尺寸下 SiC 材料的绝缘电压更高，因此相同电压电流等级下的 SiC MOSFET 能够做的更小。
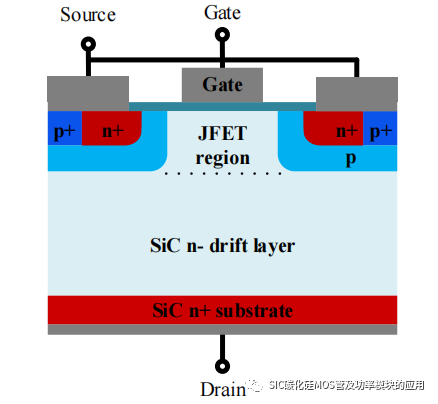
图 2-1 SiC MOSFET 的结构示意图
SiC MOSFET 仍然是一种电压控制型功率器件，当施加正栅极电压，MOSFET内部的沟道导通时，电子作为载流子穿过沟道，从 n+的源极区横向流过注入 p 阱中。之后穿过由相邻的两个 p 阱区域形成的 JFET区域，最后流经 n-漂移层到达漏极，SiC MOSFET 从电阻区进入饱和区，从而形成正向栅源极电流。当施加负栅极电压时，MOSFET 的沟道被关闭，漏源极之间存在较高的电压；MOSFET 会通过反向偏置，由 p 阱和较厚的 n-漂移层所形成的 PN 结来实现关断，SiC MOSFET 进入截止区。
SiC MOSFET 的开关模态分析
由于 SiC MOSFET 的工作频率相比于基于 Si 工艺技术的 MOSFET 更高，工作电流和电压等级更高，开通关断时间更短，因此在应用SiC MOSFET的功率电路中，相同电压电流等级下，SiC 的开通关断瞬间 di/dt 和 dv/dt 更高，输出电压和电流受到寄生参数的影响更大，因此分析 SiC MOSFET 的开通和关断的各个阶段多采用如图 2-2 所示 SiC MOSFET 寄生参数模型，模型中 Ldp、Lsp 和 Rdp、Rsp 代表着由于连接线和 PCB 布线等效的寄生电感和等效电阻；Ld、Lg和 Ls 分别表示由 SiC MOSFET的接线引脚等效的寄生电感；Rg表示 SiC MOSFET 的栅极内阻；Cgd、Cgs、Cds 分别为栅–漏、栅–源、漏–源极间电容。
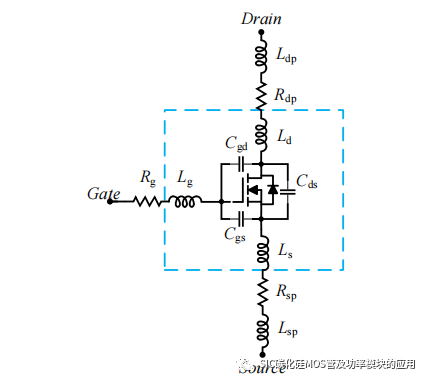
图 2-2 SiC MOSFET 器件寄生参数模型
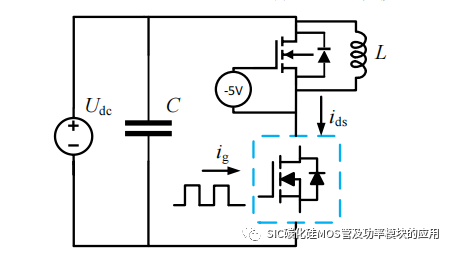
图 2-3 双脉冲测试电路等效模型
如图 2-3 所示的双脉冲测试电路，用以测试功率开关器件的开关特性电路，可以得到 SiC MOSFET 的开关各阶段电压电流的典型波形，其中 Udc 为输入的母线电压，L 为负载电感。SiC MOSFET 开通关断过程中的典型电压、电流如图 2-4 所示。其中 Vcc 和 Vee分别表示驱动 SiC MOSFET 的驱动器输出的正电压和负电压。uGS 表示 SiC MOSFET 的栅源极间电压，图中的红色波形为驱动器输出电压，黑色波形为SiC MOSFET 栅源极间电压。ids 和 uDS 分别表示 SiC MOSFET 的输出漏源极电流和漏源极间电压。
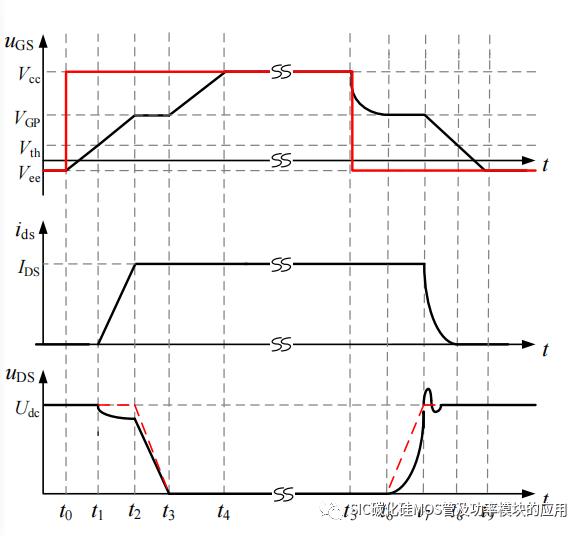
图 2-4 SiC MOSFET 的开通关断过程典型波形
图中 t0 到 t4 对应 SiC MOSFET 的开通阶段，t5到 t9 对应 SiC MOSFET 的关断阶段，具体的开通关断模态分析如下：
(1) 导通过程：
[t0-t1]阶段：当 SiC MOSFET 的驱动器输出正向驱动电压 Vcc，开始对 SiC MOSFET 的输入电容 Ciss（Ciss=Cgs+Cgd）进行充电，此时栅源极间电压 uGS 由 Vee开始上升，到达 SiC MOSFET 的导通阈值电压 Vth 之前，SiC 处于关断状态，漏源极电流 ids 为 0，漏源极电压 uDS 等于母线电压 Udc。[t1-t2]阶段：从 t1 时刻开始，栅源极电压 uGS 上升至阈值电压 Vth，此时 SiC MOSFET 进入导通状态，漏源极电流 ids 开始由 0 增加，ids 的变化可以用式(2-1)表示；由于漏源极电流 ids开始增加，变化的电流作用在寄生电感 Ld、Ldp 和 Ls、Lsp 上导致漏源极电压 uDS 出现一个电压降如图 2-4 所示，若无寄生电感，漏源极电压将会如图 2-4 中的红色虚线波形所示变化。由寄生参数导致的电压降可以用式(2-2)表示，其中 gfs 表示 SiC MOSFET 的跨导：
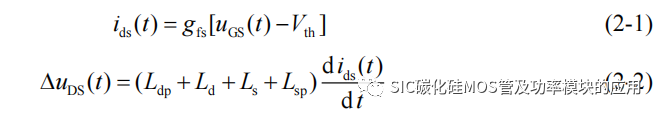
[t2-t3]阶段：由于米勒电容（栅–漏极电容 Cgd）的存在，栅极驱动电流持续为米勒电容进行充电，并保持栅源极电压 uGS 为米勒平台电压 VGP 直至充电结束。由于在米勒平台阶段，驱动电流仅给米勒电容充电，所以漏源极电压 uDS 的电压降和米勒电容电压变化近似相同，该阶段 uDS 的电压可以近似表示为：
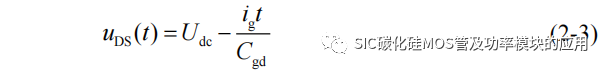
[t3-t4]阶段：t3时刻米勒电容充电结束，栅源极电压uGS上升至驱动器正电压Vcc，SiC MOSFET 饱和导通，漏源极电压 uDS 下降为 SiC MOSFET 的导通电压 UDS_on，而漏源极电流 ids 保持不变。
(2) 关断过程：
[t5-t6]阶段：t5 时刻，驱动器输出关断负电压 Vee，SiC MOSFET 开始进入关断阶段。首先栅源极电压 uGS 开始下降，此阶段栅极电流主要式由 Cgs 放电产生，漏源极电压 uDS 和电流 ids 保持不变。[t6-t7]阶段：当 t6 时刻栅源极电压 uGS 下降至米勒平台电压 VGP 后，保持该电压，米勒电容开始通过栅极电阻 RG 放电，漏源极电压 uDS 开始上升增加，并且此阶段uDS 变化率和米勒电容 Cgd 上电压变化率相同。[t7-t8]阶段：栅源极电压 uGS 持续下降，SiC MOSFET 转变为线性电阻区特性，漏源极电流 ids 开始下降，而漏源极电压 uDS 上升至母线电压后，由于寄生电感的作用，导致了关断电压过冲，过冲电压的大小可以用式(2-2)表示。当栅源极电压 uGS下降至阈值电压 Vth，此时 SiC MOSFET 完全关断，漏源极电流也下降至 0。[t8-t9]阶段：从 t8 时刻开始，ids 就已经完全为 0，SiC MOSFET 完全截至，之后栅源极电压持续减小，直至驱动负电压 Vee。
并联 SiC MOSFET 电流均衡过程分析
由于 SiC MOSFET 现有工艺技术的限制，单体 SiC MOSFET 的电流容量存在上限，因此在一些大功率高电流等级应用场合中，SiC MOSFET 的并联连接使用是一种经济高效的提升电流容量的解决方案。然而对于 SiC MOSFET，在开通关断过程中流过并联功率器件的电流会由于器件自身寄生参数不匹配和线路的不对称而不可避免地导致瞬态的电流不平衡，这种不平衡的电流对于并联的 SiC 器件的安全性和稳定性都提出了挑战。因此研究造成 SiC MOSFET 并联电流不均衡的因素可以有效地为 SiC MOSFET 并联应用设计提供参考，避免由于各类寄生参数造成的并联电流不均衡。
根据上节中关于 SiC MOSFET 的导通和阻断过程分析，可以将 SiC MOSFET 的输出漏源极电流 ids 总结如下：
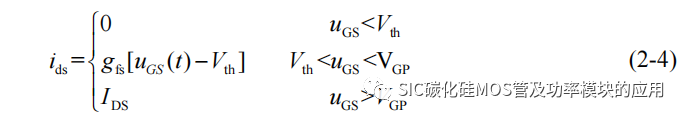
从公式(2-4)中可以发现漏源极电流 ids 主要包含两个阶段，第一阶段为栅源极电压 uGS 达到阈值电压 Vth 后，漏源极电流 ids 由 0 上升和第二阶段，当栅源极电压 uGS达到米勒平台电压后，SiC MOSFET 达到稳定输出电流，因此针对并联的 SiCMOSFET 的电流均衡过程可以对应为动态均流过程（第一阶段）和静态均流过程（第二阶段）。因此根据两个均流阶段过程进一步分析影响并联电流均衡的因素。
并联 SiC MOSFET 动态均流阶段分析
从电流公式(2-4)可以看出，在动态均流阶段，并联电流差异的影响因素主要有跨导 gfs、阈值电压 Vth 和栅源电压 uGS。对于 SiC MOSFET 而言，跨导和阈值电压属于其自身器件特性，主要受到生产工艺和温度的影响，而 uGS 则会受到更多寄生参数的影响，首先对 uGS 进行的数学建模分析。
为了便于分析，将图2-3 所示的电路进一步简化，得到如图 2-5 中左侧的简化模型，其中 D 点和 S 点之间的电压 VDS 为包含寄生参数后的 SiC MOSFET 的等效漏源极电压，当 SiC MOSFET 栅源极电压 uGS 大于阈值电压 Vth 后，SiC MOSFET 的漏源极电流 ids 开始增加，在此之前有 VDS=uDS=Udc。
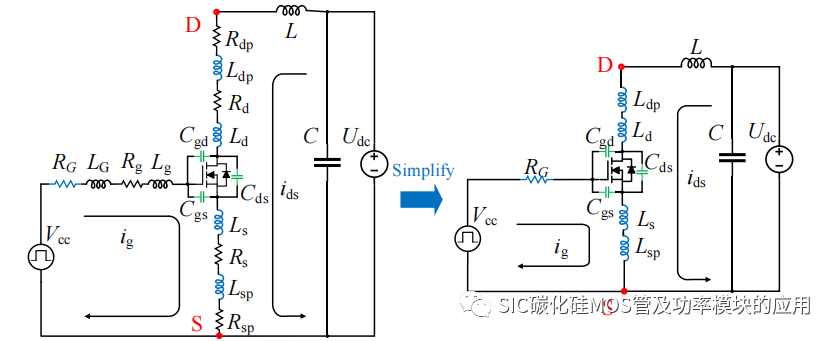
图 2-5 SiC MOSFET 开关过程等效简化模型
考虑实际应用中SiC MOSFET 多需要外加栅极电阻RG，驱动电路也靠近 SiCMOSFET 器件，因此驱动栅极的寄生电感的影响由于栅极电阻的作用可以被忽略，同时为了便于分析将驱动器的栅极电阻 RG和 SiC MOSFET 栅极内阻 Rg等效为 RG；此外由于连接线和 PCB 走线而导致的等效电阻 Rdp、Rd、Rs、Rsp 较小，相对于寄生电感的影响更低，所以得到图 2-5 中右侧的等效模型，基于此模型可列写栅极电流ig回路的基尔霍夫电压方程：
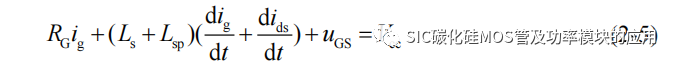
而在此阶段栅极电流 ig主要为栅–源极电容 Cgs 和栅–漏极电容 Cgd 充电，因此栅极电流 ig可以进一步表示为：
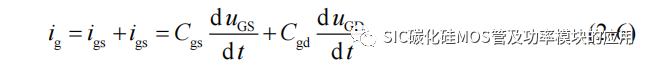
同时根据电势和电压关系，可以将uGD 表示为uGD=uGS-uDS，得到ig 的表达式：
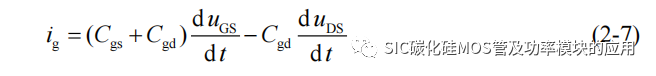
而在漏源极电流 ids 上升阶段，漏源极电压 uDS 的电压降可以表示为：
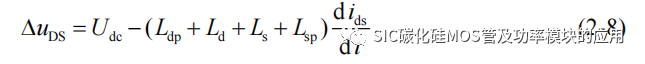
根据式(2-4)可以得到漏源极电流 ids 和栅源极电压 uGS 之间的关系：
将式(2-7)、式(2-8)和式(2-9)代入式(2-5)中，整理得到：
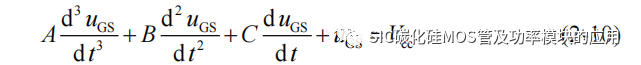
其中系数 A、B、C 分别为：
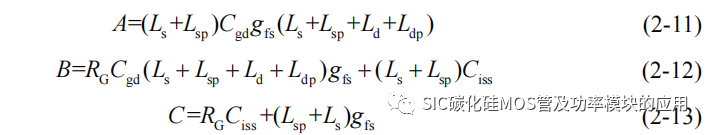
进一步求解上述微分方程即可得到栅源极电压 uGS(t)。实际由于 SiC MOSFET器件结构的原因，其栅–漏极间电容 Cgd 一般在 pF 级，并且栅源极电压三阶导函数的系数 A 中含有 Cgd、寄生电感(Ls+Lsp）和寄生电感之和(Ld+Ldp+Ls+Lsp)的乘积项，相比于系数项 B 和 C，系数 A 数量级相差 10-9，可以忽略式中三阶导数从而简化计算，带入初值条件，uGS(0)=0 和 uDS(0)=Udc 得到栅源极电压 uGS 的时域近似表达式：
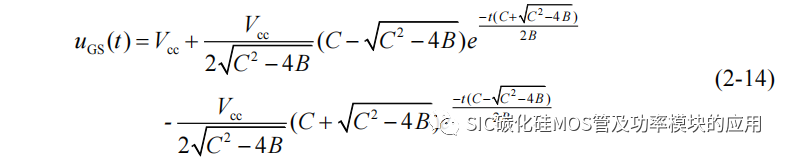
式(2-14)中的 B 和 C 的定义和式(2-12)、式(2-13)定义相同。
上述推导是针对三引脚的 SiC MOSFET 封装，如图 2-6(a)所示，这种封装下驱动回路源极和功率回路的源极共用，导致功率回路和驱动回路之间存在耦合，输出的功率电流对于驱动信号造成干扰。SiC MOSFET 往往工作于更高容量的大功率场合，为降低功率回路引起的干扰而发生误触发的现象，目前更多的 SiC MOSFET 采用如图 2-6(b)所示的封装，SiC MOSFET 的驱动源极和功率源极解耦，有效地减小功率电流回路对驱动回路的干扰。
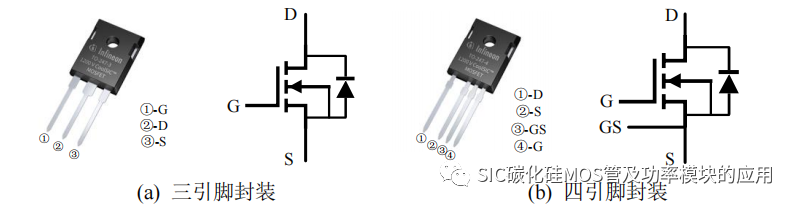
图 2-6 三引脚 SiC MOSFET 封装及等效模型
图 2-7 四引脚 SiC MOSFET 的等效开通模型
因此进一步分析四引脚封装的 SiC MOSFET 的 uGS 的时域表达式，对比两种封装下的栅源极电压区别，将四引脚的等效参数模型代入开通过程等效电路模型中，得到如图 2-7 所示的简化模型，模型中 Lsg为驱动源极引脚等效寄生电感，针对栅极电流 ig列写驱动回路的基尔霍夫电压方程：
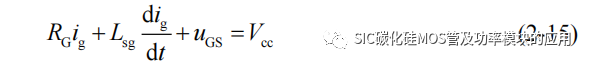
等式(2-7)、(2-8)、(2-9)代入(2-15)中，可以得到：
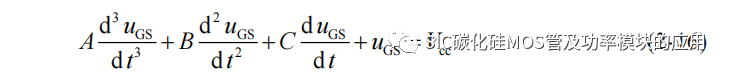
其中 A、B、C 的定义为：
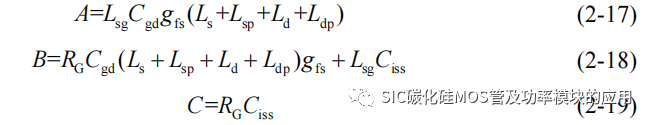
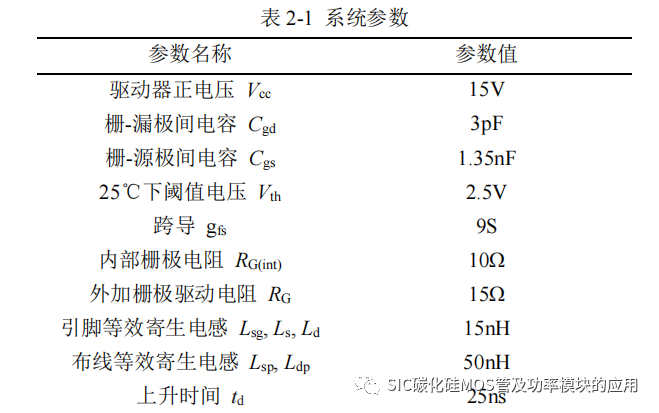
同理，由于三阶导数项系数相比其他项系数较小，为简化计算，忽略三阶导数项求解微分方程，得到和式(2-14)相同形式的解析解，式中 B 和 C 的定义为式(2-18)和式(2-19)，对比两种封装下的栅源极电压 uGS 系数，可以发现二阶导数项系数基本相同，而一阶导数项的系数表达式，四引脚封装的相比于三引脚封装少了(Ls+Lsp)gfs项，可以看出将驱动源极和功率源极分开后，栅源极电压收到源极寄生电感的影响变小。可以有效地降低功率环路对于驱动信号的干扰。由于栅极电压公式(2-14)只是栅源极电压达到米勒平台电压 VGP 前的表达式，即对应于图 2-4 中 t0-t2的阶段，此阶段 SiC MOSFET 的动态均流主要受到栅源极电压影响，为验证求解的 uGS 时域表达式的准确性，将求解得到的四引脚封装 SiC MOSFET 的栅极电压时域表达式，代入如表 2-1 所示的器件参数，参数来源于 CREE公司的 C3M0075120K 数据手册，并在 Matlab 软件中绘制其波形，得到如图 2-8 所示的栅源极电压 uGS 和输出漏源极电流 ids 的近似波形。对比图 2-9 所示的，基于C3M0075120K 的双脉冲测试开通过程中 UGS和 IDS 波形，可以发现在动态均流阶段的栅源极电压的变化趋势是基本一致的。
进一步分析各个参数对并联 SiC MOSFET 动态均流过程的影响，假设除被分析参数外，其他器件参数相同：
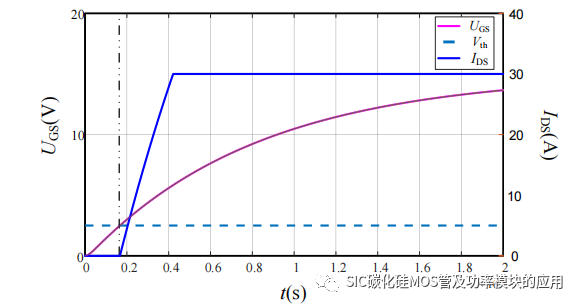
图 2-8 四引脚 SiC MOSFET 的理论 uGS 和 ids 波形
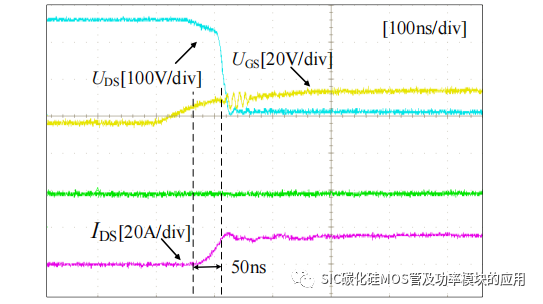
图 2-9 SiC MOSFET 开通过程 UGS 和 IDS波形
(1) 阈值电压 Vth：阈值电压将决定 SiC MOSFET 的导通和关断时间，Vth 小的SiC 器件会优先导通，同时关断过程中也会延迟关断，在整个导通期间承担输出电流的时间更长。根据电流 ids 和 Vth 之间的关系式(2-4)可知：并联动态均流差异 Δids和阈值电压差异 ΔVth 成正比。如图 2-10(a)所示，为相同栅源极电压下的开通过程中20ns 到 30ns 区间，Vth 从 2.5V 变化到 3.5V 输出漏源极电流 IDS 的变化趋势；图 2-10(b)为并联 SiC MOSFET 的动态均流差异 Δids 随阈值电压差异 ΔVth 和时间 t 的变化趋势。从图中可以发现当阈值电压增加后，开通过程延迟，阈值电压小的 SiCMOSFET 会优先导通，此时并联的 SiC MOSFET 的 uDS 会降低，因此优先导通的电流和电压都高于其他并联 SiC MOSFET，承受更高的开关损耗。但是 SiC MOSFET损耗增加，导致结温上升，阈值电压随温度上升而增加，进而可能实现开通关断的一致性。
(2) 栅–漏极间电容 Cgd：当并联的 SiC MOSFET 的 Cgd 偏大时，会造成 uGS的上升变缓，输入电容 Ciss 的充电时间边长。如图 2-11(a) 所示，为 Cgd 从 3pF 变化到40pF 时，uGS 随 Cgd 和时间 t 变化的曲线；图 2-11(b) 所示为动态均流不平衡电流Δids 随着 Cgd 和 t 变化的曲线。从图中可以看出，尽管当 Cgd 存在 40pF 的差异时，会导致栅源极电压存在最大 1V 的偏差，但 Δids 却达到 10A，且该电流差异的是随时间变化逐渐减小的，如图 2-11(b) 所示，当电容的差异存在 40pF，t 从 10ns 到20ns，动态电流差异从 9.29A 减小到 8.1A。实际中，SiC MOSFET 晶圆的结构和 SiC材料的特性决定 Cgd 较小，差异一般在几 pF，对于动态均流的影响并不会很大。
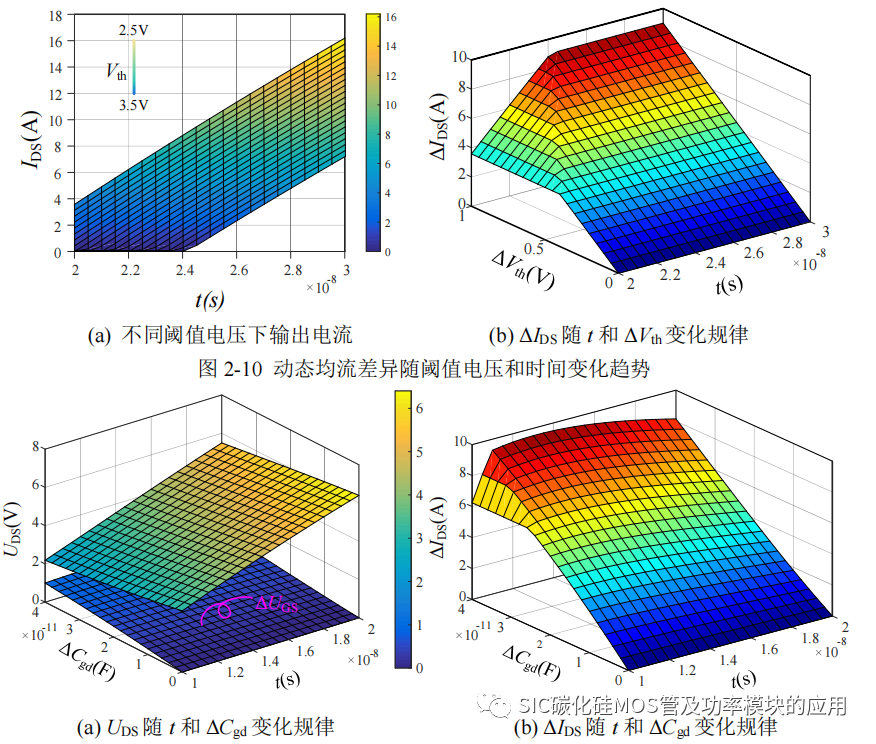
图 2-11 栅–漏极间电容 Cgd 对栅源极电压和动态均流的影响
（3)栅–源极间电容 Cgs：和 Cgd 类似，当 Cgs较大时，会造成充电时间延长,导致 uGS 上升缓慢，从而造成动态均流差异，但 Cgs 作为输入电容 Ciss 的主要部分，一般大小在 nF 级别，相比于 Cgd，Cgs 对栅源极电压和动态均流的影响更大。如图 2-12 所示为 uGS 和 Δids 随时间 t 和 Cgs 的变化趋势曲线。曲线是 Cgs 从 0pF 变化到0.5nF，截取 10ns 到 20ns 阶段的 uGS 和 ids 的变化趋势，图 2-12(a)中的 UGS1 为含有Cgs 变化的栅源极电压波形，UGS2 为 Cgs 保持不变的的栅源极电压，对比两个栅源极电压波形，可以发现当 Cgs 变大后，uGS 上升变缓，且随着时间的累加，uGS 和动态均流差异逐渐拉开。因此 Cgs 在动态均流过程中的影响相比于 Cgd 更大，然而实际应用中，由于并联的SiC MOSFET采用同一驱动器进行驱动，并且加入栅极吸收电路，引入了其他的等效寄生电容，为了保证电路的对称性和一致性常外加额外的电容来实现并联的 SiC MOSFET 的 Cgs 均衡，从而消除 Cgs 的不对称造成的影响。
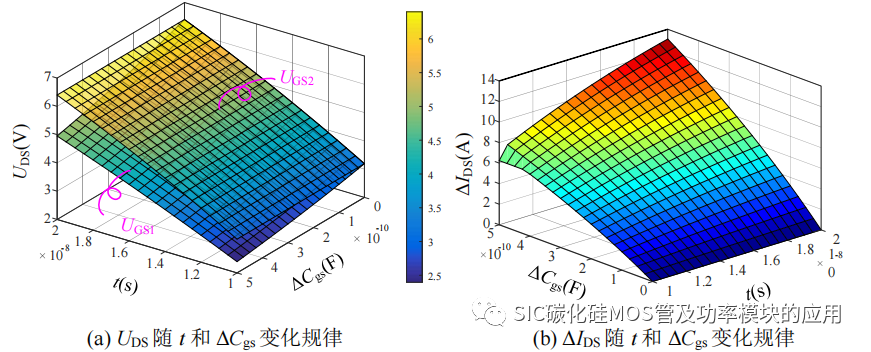
图 2-12 栅–源极间电容 Cgs对栅源极电压和动态均流的影响
(4) 栅极驱动电阻 RG：驱动电阻主要起到限制开通充电电流和关断放电电流的作用。在实际应用中，对 SiC MOSFET 需要外加驱动电阻，回路驱动电阻差异主要是由于器件本身栅极内阻造成。如图 2-13 所示为驱动电阻差异从 0Ω 变化到 4Ω 导致栅源极电压和动态均流不平衡的波形。从图 2-13(a)可以看出，当栅极电阻差异ΔRG 达到 4Ω 时，栅源极电压差异最大不超过 1V，但是造成的动态并联电流差异Δids 却达到接近 3A，并随时间逐渐增加。因为栅极电阻限制了栅极充、放电电流，造成了并联 SiC MOSFET 的栅源及电压上升速度不一致，进而逐渐造成了动态均流不平衡度加剧。
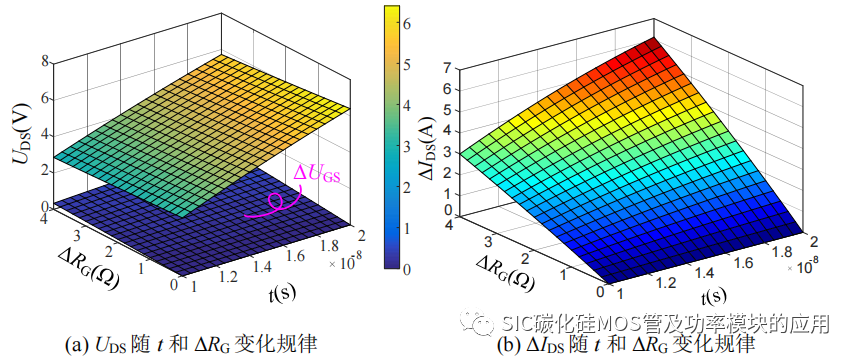
图 2-13 栅极驱动电阻 RG对栅源极电压和动态均流的影响
(5) 漏极总寄生电感 LD和源极总寄生电感 LS：根据得到 uGS 的时域表达式,在uGS 的上升阶段，无论是漏极寄生电感还是源极寄生电感都是以(Ls+Lsp+Ld+Ldp)的形式存在，其对动态均流的影响都是一致的，所以将寄生电感统一为 LP 分析其对 uGS的影响。由于 SiC MOSFET 的器件封装是一致的，引脚的长度、宽度都是相同的，所以引脚等效的寄生电感 Ls、Ld、Lsg等都是基本不变的，造成额外寄生电感的主要原因是连接引脚的 PCB 覆铜或走线。根据文献[68-70]等，可以大致估算出器件引脚等效寄生电感，即 Ls、Ld、Lsg等大约为 10nH。如图 2-14 所示为，当寄生电感 LP 增量由 0nH 变化到 500nH 的过程中，栅源极电压 uGS 和动态电流差异 Δids 随时间 t 和寄生电感差异 ΔLP 变化趋势曲线。从图中可以看出，尽管 ΔLP 最大达到 500nH，而对应造成的动态均流差异仅为 3A，且随着时间的增加，动态均流差异在逐渐减小，因此在动态均流过程中，寄生电感的差异实际影响较小。在保证并联直流对称的情况下，可以消除由 ΔLP 造成的动态电流不均衡的现象。
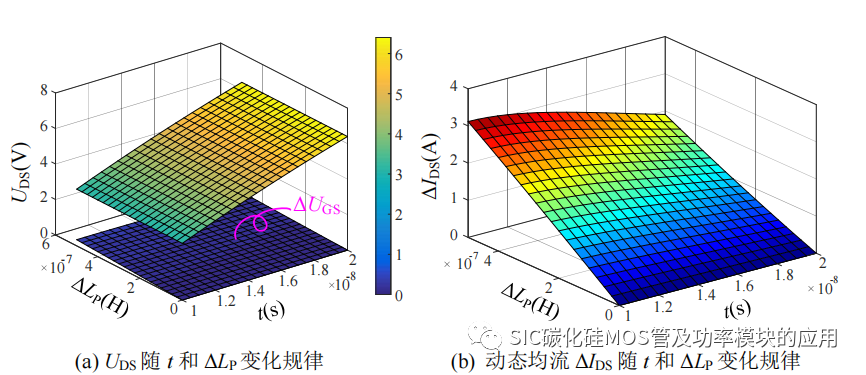
图 2-14 寄生电感 LP 对栅源极电压和动态均流的影响
动态均流过程的电流不平衡会加剧开关过程的开关损耗，并且动态电流的不均衡会影响到静态均流的初始过程，而加剧通态损耗，因此应尽可能降低动态均流差异。综上分析，在动态均流阶段，对于 SiC MOSFET 器件自身的寄生参数，由生产工艺和批次所决定，因此对于 RG、Cgs、Cgd 造成的并联 SiC MOSFET 动态均流差异，可以依靠驱动电路和功率电路的布局一致性实现降低动态电流不均衡程度，甚至实现完全动态均流。而寄生电感对于动态均流的影响相较小，保证并联支路的结构对称可以有效降低寄生电感差异。
并联 SiC MOSFET 静态均流阶段分析
当栅源极电压 uGS 等于米勒平台电压 VGP，此时 ids 就已经达到输出稳定电流，此时并联的 SiC MOSFET 进入静态均流阶段，在静态均流阶段，SiC MOSFET 进入完全导通状态，可以等效为导通电阻，并联 SiC MOSFET 可以等效为如图 2-15 所示的模型，并联 SiC MOSFET 等效为导通电阻 Rds1 和 Rds2；当 SiC MOSFET 完全开通后，栅源极电压 uGS 对 SiC MOSFET 的影响降低，并且很短时间内 Cgs 和 Cgd 将会被充满，此时并联输出电流 ids1、ids2 主要受到寄生电感 LD 和 LS 的影响，并且会保持动态均流结束阶段的差异电流 Δids(td)，其中 td 为在动态均流阶段 uGS 的上升时间，即 ids 的上升至输出电流的时间。
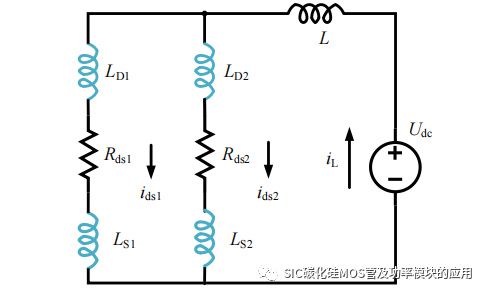
图 2-15 静态均流简化模型
结合电路具体分析寄生电感在静态均流过程中的影响：根据电路中电流回路和电压关系可以得到：
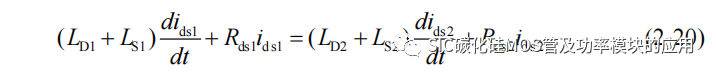
由于源极和漏极的寄生电感的作用相同，设 LP=LD+LS，设并联支路之间的寄生电感关系为：LP1=LP2+ΔL，ΔL 表示并联支路间的等效寄生电感总差异；假设除寄生电感存在差异外，其他参数维持不变，则设导通电阻 Rds1=Rds2=Rds，另设并联支路电流关系为：ids1=ids2+Δi，则关系(2-20)可以表示为：
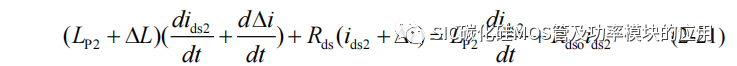
SiC MOSFET 的导通电阻很小，相比于传统的 Si 功率器件，导通电阻仅100mΩ左右，因此其导通电压相比于母线电压很小，所以可以近似得到导通后的直流母线电压关系：
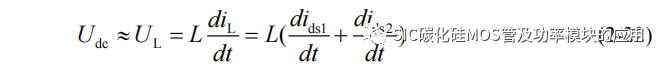
将并联支路电流关系代入上式，可以得到输出电流的导数关系：
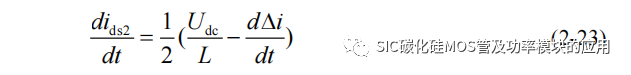
最后得到并联电流差异 Δi 的微分方程：
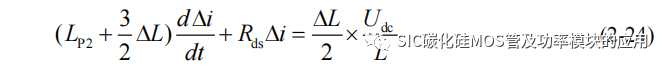
代入微分方程的初值条件，Δi(0)=Δid(td)，Δid为动态均流过程中的均流差异，
td 表示电流的上升时间，可以得到静态均流差异和寄生电感差异与时间的关系：
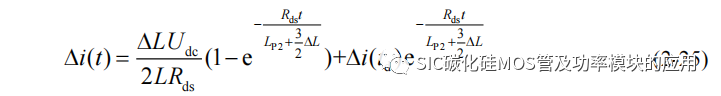
从上述静态均流的时域表达式可以看出，静态均流差异是一个随着时间趋于稳定的形式，且动态均流差异项也是随着导通时间的增加而逐渐衰减，稳态时只会保留静态均流差异部分。如图 2-16 所示为并联均流随时间和寄生电感差异变化的曲线，其中图 2-16(a)为 15ns 和 30ns 两种情况下的动态均流差异随寄生寄生电感变化情况，其中寄生电感差异由 0nH 到 500nH 变化，由于上升时间较长，所以动态不均衡电流相对较大；进入图 2-16(b)所示的静态均流阶段的并联均流差异无论动态均流差异项的大小，在大约 20μs 后，在同一寄生电感不均衡的条件下，由寄生电感引起的静态均流差异趋于一致。而此过程中动态均流的不均衡电流会逐渐缩小，转变为静态均流不均衡。
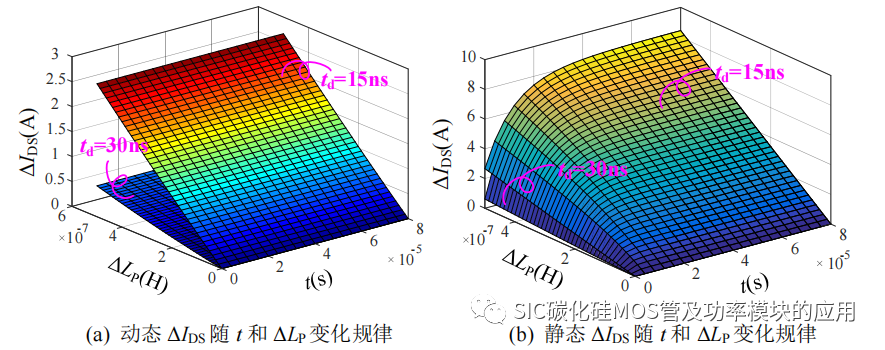
图 2-16 静态均流变化随时间和寄生电感差异变化曲线
此外，除上述分析参数外，由于阈值电压和导通电阻都是关于温度的函数，温度对于静态均流和动态均流过程也具有较大影响，且温度受到导通损耗和环境因素影响较大，故本节不做详细分析，将在第三章进行相关的分析和讨论。基于上述分析，消除并联均流差异，不仅需要保证器件参数的对称，消除动态均流过程中的动态均流差异，同时保证并联支路的对称，降低电路等效寄生电感来实现并联 SiC MOSFET 的静态均流，确保开通损耗和开关损耗的最低。
实验验证及结果
为了研究寄生参数对并联 SiC MOSFET 的均流过程的影响，搭建了如图 2-17所示的 SiC MOSFET 并联均流测试硬件平台，用以测试存在不同寄生参数差异的情况下，对动态均流和静态均流的影响。电路的拓扑为半桥电路，采用上下桥臂采用SiC MOSFET 并联的方式，并且为了保证电路寄生参数的对称，所以并联支路采用完全对称的布局方式，并预留有接入寄生电感和其他寄生参数的接入端口。
图 2-17 并联 SiC MOSFET 均流实验平台
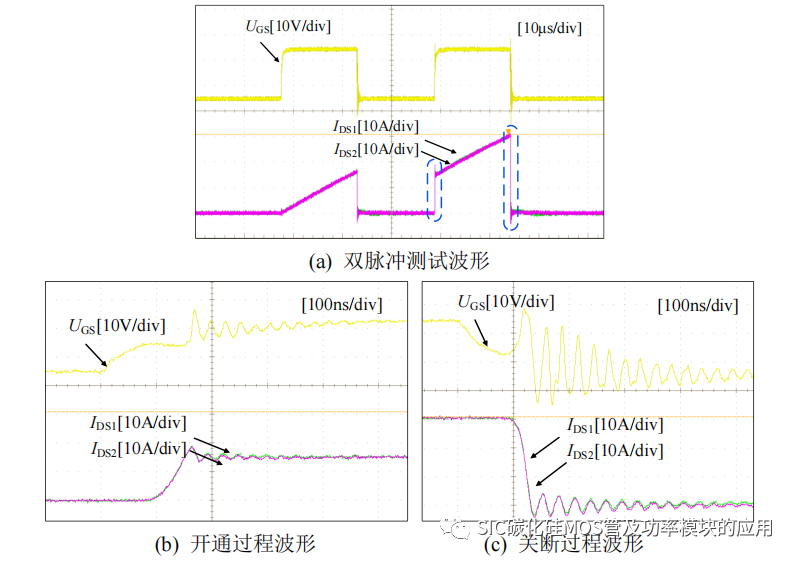
图 2-18 无寄生参数下的并联 SiC MOSFET 均流波形
为了和第二节分析动态和静态均流趋势使用的参数保持一致，实验平台采用的SiC MOSFET 为 CREE 公司的第三代 SiC 器件 C3M0075120K，利用平台搭建如图2-3 所示的双脉冲测试电路，利用第二个脉冲过程观察并联 SiC MOSFET 的静态均流和动态均流验证寄生参数的影响。设置测试条件为 250V 母线电压，负载电感选用 120μH 的负载电感，脉冲参数为周期 25μs，占空比 50%的两个脉冲。为了验证MOSFET 并联支路的寄生参数对称性，首先不添加额外的寄生参数的条件下进行测试，并联的 SiC MOSFET 利用同一个驱动器进行驱动，驱动电阻为开通过程 16.5Ω，关断电阻 11.5Ω，并且都增加了 2.2nF 的栅–源极电容，用以抑制驱动电压震荡。无外加寄生参数条件下的均流波形如图 2-18 所示。图 2-18(a) 为两个脉冲下的整体波形，图 2-18(b) 和图 2-18(c) 为开通和关断瞬间的均流波形，从波形来看，在没有任何外加寄生参数的情况下，对于并联的 SiC MOSFET，无论是静态均流过程还是动态均流过程，并联支路电流都是几乎一致的。因此可以验证该电路设计是结构对称的，并且并联 SiC MOSFET 支路的寄生电感是一致的。在此基础上人为添加寄生参数对比动、静态均流情况。
2.4.1 Cgd对动态均流影响实验
测试 Cgd 对于动态均流的影响，在对称电路的基础上，对 SiC MOSFET2 外加Cgd 电容，如图 2-19 所示为无外加 Cgd 下的动态均流波形，其中绿色波形为 SiC MOSFET2 对应的 IDS2，紫色为 SiC MOSFET1 对应的 IDS1（之后的实验中电流波形颜色定义相同）。图 2-20 所示为对 SiC MOSFET2 的 Cgd 外加 101 电容后的动态均流的波形。
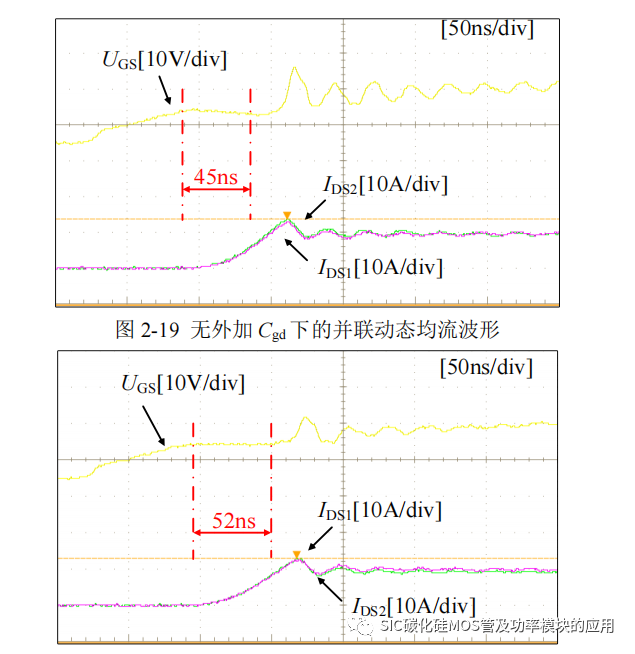
图 2-20 Cgd 外加 101 电容下的动态均流波形
在对并联的 Cgd 逐渐增加电容的过程中，发现较大的 Cgd 差异对动态均流差异并没有太大的影响，但是在逐渐增加 Cgd 的过程中，驱动电压的米勒平台持续时间增大，如图 2-19 所示，无外加 Cgd 时，米勒平台电压时间大约为 45ns，增加 101 电容后，米勒平台时间增加到 52ns，但是最大动态均流差异仍在 0.4A 左右，几乎没有变化。因此 Cgd 对于并联 SiC MOSFET 的动态均流过程影响很小，也说明在动态均流栅源极间电容为 Cgs 占据栅极电流。
2.4.2 Cgs对动态均流影响实验
测试并联 SiC MOSFET 的 Cgs 存在差异时，对并联动态均流的影响，首先将SiCMOSFET 驱动电路的栅极辅助电容取下，测得此时的动态均流波形如图 2-21(a)所示，之后保持 SiC MOSFET1 无外加 Cgs 的状态下，逐渐增加 SiC MOSFET2 的 Cgs，依次得到如图 2-21(b)到(d)的三组动态均流波形，其中图 2-21(b)为在 SiC MOSFET的栅源极外加 2.2nF 的电容下的动态均流波形，图 2-21(c)为外加 4.7nF 的电容下的动态均流波形，图 2-21(d)为 22nF 下的均流波形。
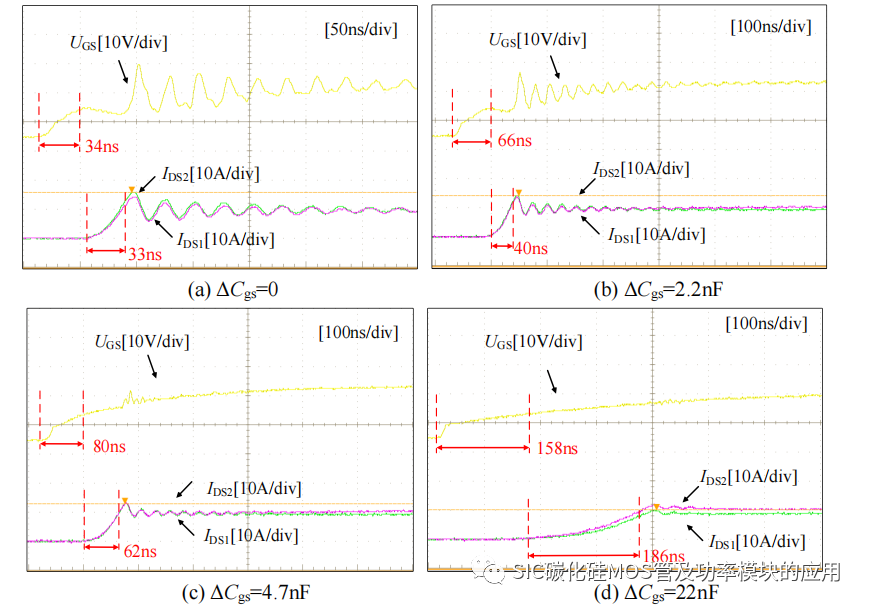
图 2-21 Cgs 差异下动态均流差异波形
从测得的动态均流波形可以看出，并联 SiC MOSFET 都无外加 Cgs 时，其动态均流存在一定差异，且驱动栅源极电压和电流开通过程的电流震荡幅值和频率较高，都是由于此时的寄生参数较小，造成的谐振频率较高；当不平衡栅–源极电容 ΔCgs从 47pF 到 22nF 逐渐变化的过程中，栅极驱动电压上的震荡幅度和频率逐渐减缓，当达到 22nF 时，基本消除了开通过程的电流震荡驱动电压震荡；但伴随着震荡的缓解，开通过程的持续时间和输出电流 IDS的上升时间也随之增加。如图 2-21 所示，当无外加 Cgs 时，栅源极电压 UGS 从零到阈值电压的上升时间约为 34ns，电流上升时间约为 33ns，且动态均流效果较好；当 ΔCgs=2.2nF 时，动态均流相比无 ΔCgs 的情况，几乎没有什么变化，而 UGS 的上升时间增加到了 66ns，电流的上升时间也略有增加；当 ΔCgs=22nF 时，才开始出现电流不均衡现象，但动态均流差异，从 0A 开始随时间加剧，到最大 2A 的不均衡度，此外 UGS 和 IDS的上升时间都超过了 100ns。Cgs 的差异对于动态均流的影响较小，实际中对并联的 SiC MOSFET 会在栅源极外加辅助电容消除震荡，也变相地抑制了 Cgs 对动态均流的影响，但要注意过大的 Cgs 会造成导通时间增加，会加剧开通损耗。
2.4.3 RG对动态均流影响实验
驱动电阻 RG 主要在开通和关断时起到限制充电电流和放电电流的作用，对于并联的 SiC MOSFET 的动态均流有较大的影响。在保留驱动器 10Ω 的公共驱动电阻，依次为 SiC MOSFET2 放置额外的驱动电阻 ΔRG，得到如图 2-22 所示不同 ΔRG下的并联动态均流波形。
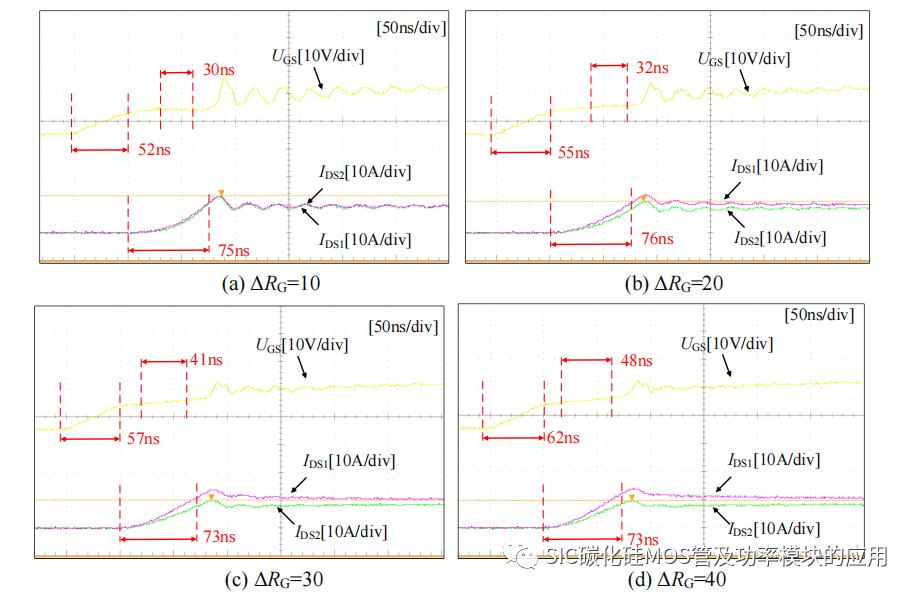图 2-22 驱动电阻差异对动态均流的影响
对比四组不同 ΔRG的动态均流波形，可以发现，驱动电阻对在导通过程中，会对 UGS 造成上升延迟，当 ΔRG从 10Ω 变化到 38Ω 时，UGS 会增加 3ns-5ns 的延迟上升时间，才能达到阈值电压；之后由于栅极电阻限制充电电流，米勒平台的持续时间也会相应增加，但影响相对较小。具体的动态均流差异在不同 ΔRG 下的波形如图2-23 所示，图中 0 点为测试时设置的触发条件，标志着 SiC MOSFET 开始导通时刻，可见 ΔRG对动态均流的影响是非线性的，此外在电流上升阶段动态均流差异随着时间累计，当达到由于寄生电容电感造成震荡峰值时，达到最大电流差异，此后进入静态均流阶段，静态均流开始趋向均衡。
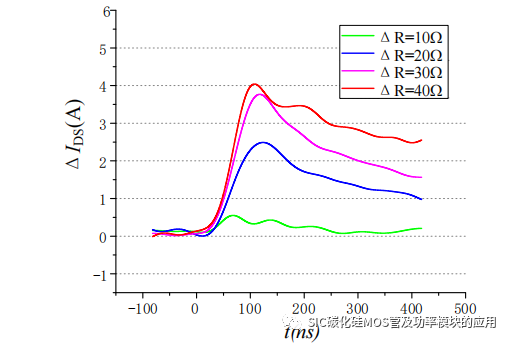
图 2-23 动态均流差异随驱动电阻差异变换波形
如图 2-24 所示，为 47Ω 驱动电阻差异下的开关瞬间动态均流情况，可以看到由于 SiC MOSFET2 的驱动电阻较大，电流缓慢上升；关断之前可以看到在静态均流过程中由于不存在其他的寄生参数的影响，并联 SiC MOSFET 静态均流；关断瞬间，SiC MOSFET1 的栅源极电压泄放的速度更快，最先达到阈值电压而关断，此时SiC MOSFET2 未关断，开始分担更多的输出电流，之后 uGS2 降低到阈值电压之下，SiC MOSFET2 才开始关断，电流下降。因此栅极驱动电阻差异 ΔRG 不仅在开通过程会造成动态电流的不均衡，在关断过程对于动态均流的影响依旧存在。
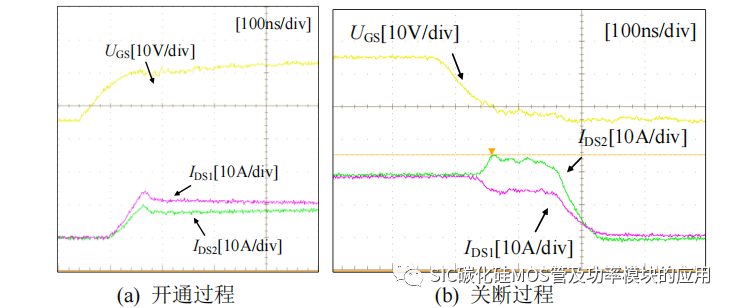
图 2-24 47Ω 驱动电阻差异下的开通和关断过程动态均流波形
2.4.4 LD和 LS对动态均流影响实验
由于寄生电感的感性作用，会对电流起到抑制作用，因此在均流过程中，寄生电感大的并联支路电流会先对电感进行充电，导致电流增长缓慢，因此漏极寄生电感 LD和源极寄生电 LS都会造成动态均流的不平衡，如图 2-25 所示为由 LD和 LS 不均衡条件下的的动态均流波形，其中 IDS1 为寄生电感较小的 SiC MOSFET1 支路电流。图 2-26 为动态均流差异在不同寄生电感差异条件下的波形。
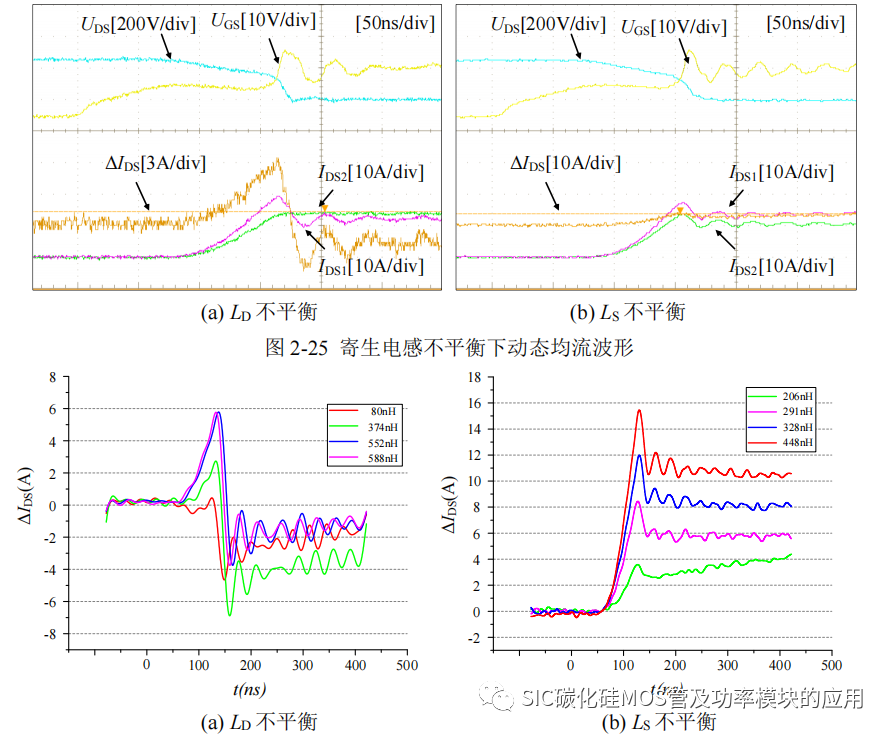
图 2-26 动态均流差异趋势波形
从图 2-26 可以看出，随着寄生电感不均衡度的增加，动态均流差异也随之增加，且开通瞬间由于寄生电容和电感之间谐振造成的电流过冲更高，且从图 2-25 中可以看出，在动态均流阶段，均流差异曲线的斜率是基本逐渐变缓的；漏极寄生电感的引入也会减缓导通过程的电流增长速度。
2.4.5 LD和 LS对静态均流影响实验
进一步比较静态均流阶段寄生电感的影响，由于电感的感性作用对于电流是一种阻碍作用，当 SiC MOSFET 从开关状态切换过程的中，漏极寄生电感 LD 和源极寄生电感 LS 都会对电流存在阻碍作用，造成关断过程的滞后。如图 2-27 所示，为存在的 ΔLD和 ΔLS 两种情况下的并联 SiC MOSFET 并联静态电流波形，其中两组波形都是为 IDS2 表示含有更大寄生电感的 SiC MOSFET 支路电流。图 2-28 所示为静态均流差异随着寄生电感变化的波形。
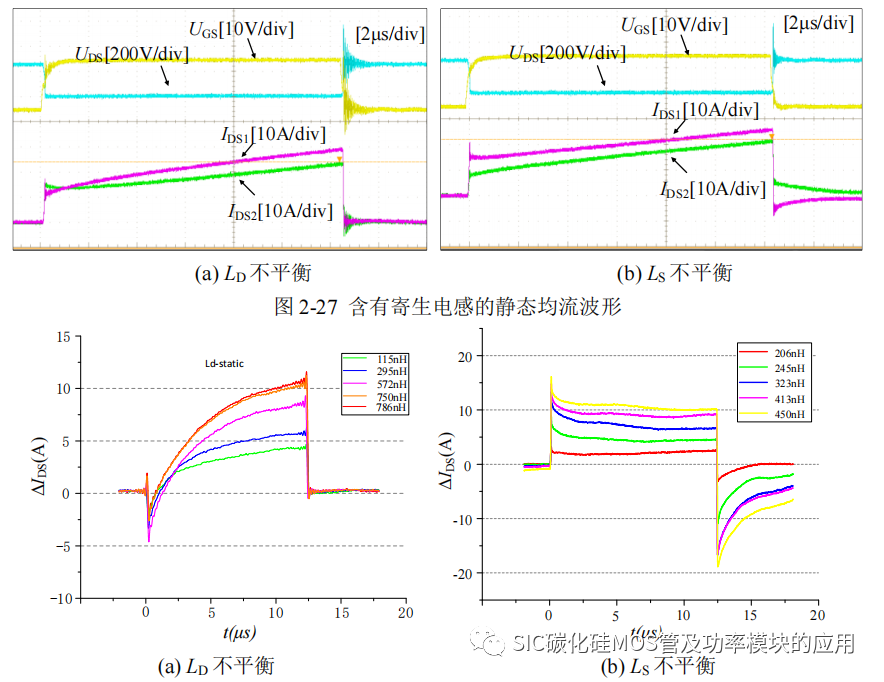图 2-28 不同寄生电感下的静态均流差异
从图 2-28 可以看出，当寄生电感的差异固定时，静态均流差异是一个趋于稳定的值；根据图 2-28(a)，在当存在较大 ΔLD时，开通瞬间会出现静态电流差异为负的情况，即 LD 大的支路电流更大，这是由于电感的感性作用和会阻碍电流的变化趋势，当导通后 LD中储存的能量会进行泄放，电流开始趋于稳态均流值，漏极寄生电感越大，趋于稳定静态均流差异所花费时间越长；同理如图 2-28(b)，LS 不均衡时，当 ΔLS 大的，会在刚导通时刻电流差异会出现一个下降的阶段，是对于 LS 进行充电造成，而关断时，存储在 LS 中的能量会阻碍电流的跌落，寄生电感中的电流泄放电流，导致电流差异负值的出现，而实际 SiC MOSFET 的驱动电压已经低于导通阈值电压，SiC MOSFET 已经关断，ids 为 0，其关断后的电流则为寄生电感的电流输出，通过驱动源极的连接进行续流，所以出现负电流。
综合比较各个参数对于均流的影响，在动态均流阶段，可以依靠驱动电路参数的一致性有效地消除动态均流不平衡；但在静态均流阶段，寄生电感仍是对影响均流效果的主要因素，保证并联支路的完全对称可以实现静态均流，当由于特殊原因导致并联支路无法对称时，就需要采用降额法、阻抗串联或串联耦合电感等外接无源器件的方式来保证静态均流。
2.5 本章小结
本章节中，首先结合并构建的 SiC MOSFET 的寄生参数模型，给出了 SiCMOSFET 的工作原理和开关状态波形，推导了开通关断过程的输出电流表达式，根据输出电流的数学表达式确定在动态均流和静态均流阶段影响均流情况的寄生参数，并绘制了参数差异和电流差异之间的关系曲线；最后在实验平台上，验证了栅源极电容 ΔCgs、栅漏极电容 ΔCgd、驱动电阻 ΔRG、漏极寄生电感 ΔLD 和源极寄生电感 ΔLS 对动态均流和静态均流过程中电流不均衡程度的影响。从实验结果可以发现尽管动态均流受到的影响因素较多，但可以依靠驱动电路的一致性来弥补；但静态均流差异对寄生电感及输出电流更为敏感，因此保证并联支路的对称为首选的有效消除寄生电感差异带来不均衡电流的方式。
第 3 章 器件损耗对 SiC 均流特性影响研究
3.1 引言
SiC MOSFET 具有正文特性，可以实现并联电流均衡，本章以基于 SiC MOSFET半桥模块的 Boost 电路，首先给出了 SiC MOSFET 的开关损耗和导通损耗的计算方法，其次分析了温度对于导通电阻和阈值电压的影响，进一步分析了温度对并联均流和损耗分配的影响。基于 PLECS 仿真软件对上述问题进行了仿真验证。
3.2 SiC MOSFET 器件损耗分析
SiC MOSFET 器件的优势在于其高击穿电压，相同电压等级下的 SiC MOSFET器件可以做到更小，导通电阻更低，因此可以有效地提升电路效率，提升电路的功率密度。为了进一步量化分析采用 SiC MOSFET 代替 Si IGBT 器件带来的效率提升，对 SiC MOSFET 驱动周期内产生损耗进行分析。
3.2.1 SiC MOSFET 损耗定义
SiC MOSFET 作为电力电子功率器件，其主要处于开关状态，因此 SiC MOSFET应用过程产生的器件损耗主要包括开关损耗和导通损耗。如图 3-1 所示，其中(a)为由半桥模块构成的 Boost 电路，基于该电路来说明一个 SiC MOSFET 的开关周期内的器件损耗；如图 3-1(b)所示为一个开关周期内 SiC MOSFET 的器件损耗定义，当UGS 由高变为低时，Q2 关断，此时产生关断损耗 Poff；Q2 关断期间，SiC MOSFET体二极管 D1 进行续流，Pcon_D 为 D1 的导通损耗；当 UGS 变为高，Q2 开始导通，在逐渐导通的过程中，首先产生开通损耗 Pon，之后 D1 关断，由于二极管的反向恢复电流，导致反向恢复损耗 Prec_D，之后 Q2 持续导通，产生导通损耗 Pcon，以上为 SiCMOSFET 一个工作周期内的损耗定义。
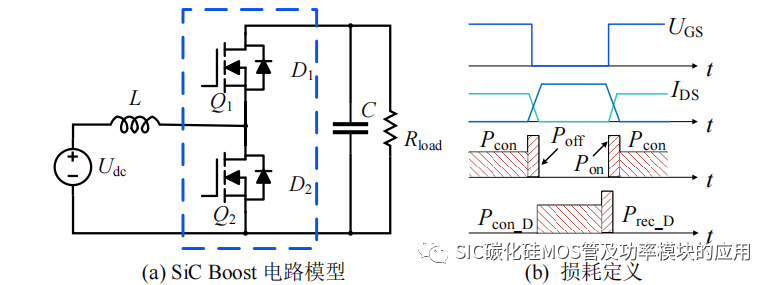
图 3-1 SiC MOSFET 的器件损耗
相比于 Si 功率器件，SiC 功率器件的工作频率更高，开通关断时间更短，导通电阻更小，因此其开关损耗和导通损耗都将比相同容量下的 Si 功率器件电路更小。
由第二章的分析可知，在开关过程中，SiC MOSFET 的输出电流和电压受到寄生参数的影响更大，导通损耗和开关损耗的计算也不同于以往的 Si MOSFET 的损耗计算公式。在 Si 功率器件的损耗分析中，对于开关损耗常用式(3-1)进行计算，其中 ton 和toff 分别表示导通和关断过程持续的时间：
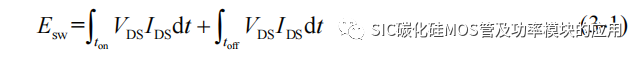
其中前半部分为开通损耗，后半部分为关断损耗，然而根据文献[71-73]的研究表明，在实际开通和关断的瞬态过程流过“电阻性”沟道的电流不只包含输出漏源极电流IDS，因此引入 SiC MOSFET 的沟道电流 ICH，作为 SiC MOSFET 的损耗电流。在开通过程的米勒平台阶段，输出电容 Coss 的放电电流会流过 SiC MOSFET 内部的沟道产生功率损耗，因此开通过程的沟道电流定义为：
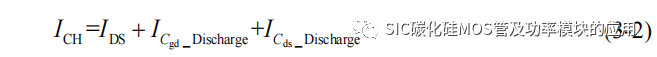
其中ICgd和ICds为开通过程中的栅–漏极间电容Cgd和漏–源极间电容Cds的放电电流。在关断过程，IDS 不仅作为输出电流，当栅源极电压小于阈值电压后，但 IDS 会为 Cgd 和 Cds 进行充电，而在 SiC MOSFET 的内部，该充电电流不会经过沟道，并不会产生相应的热损耗，因此关断过程的沟道电流 ICH可以表示为：
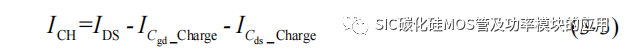
下面对 SiC MOSFET 的工作过程中的开关损耗和导通损耗等进行具体的分析。
3.2.2 SiC MOSFET 开通损耗计算
如图 3-2 所示为 SiC MOSFET 开通过程中栅源极电压、输出电流和漏源极电压的等效示意图和实际测试得到的对比波形。在此基础上对开通过程中的各阶段损耗进行分析，分析如下：
(1) t0-t1 阶段：从 t0 时刻开始，驱动信号转变为正，SiC MOSFET 开始导通，uGS(t)开始上升，此时未达到阈值电压，SiC MOSFET 不导通，电路的输出电流经过体二极管 D1 进行续流。此阶段栅极电流主要对 Cgs 和 Cgd 进行充电，为简化计算，将 uGS(t)的时域方程写为：
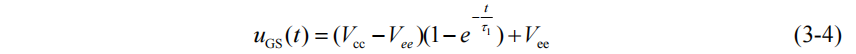
其中 Vcc 和 Vee表示驱动的正负电压，τ1 为栅极电流的充电时间常数，其大小和开通过程驱动回路总电阻 RON和 SiC MOSFET 的极间电容有关，定义为：
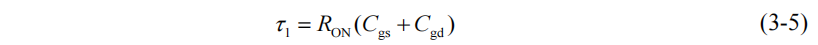
当 UGS=Vth，SiC MOSFET 开始导通，进入下一阶段。
t0-t1 阶段对应 SiC MOSFET的开通延迟阶段，依靠式(3-4)可以近似求解开通延迟时间，假设以 t0 作为时间起始原点：
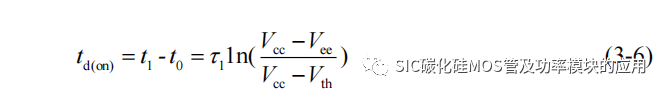
由于此阶段 SiC MOSFET 沟道未有电流流过，因此 SiC MOSFET 器件本身没
有损耗产生，该阶段内的器件损耗为二极管的导通损耗和驱动损耗。
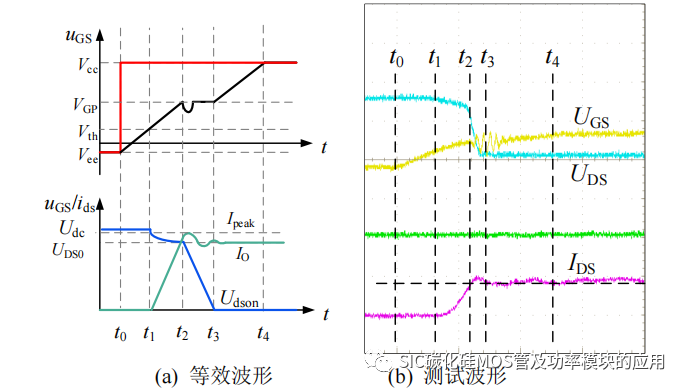图 3-2 开通过程波形图
(2) t1-t2 阶段：从 t1 时刻 SiC MOSFET 进入导通状态，此阶段的 uGS(t)的表达式依然可以用式(3-4)表示，同时 SiC MOSFET 的漏源极电流 ids(t)可以表示为：
当 IDS 达到电路输出电流 IO时，栅源极电压进入米勒平台，此时 uGS=VGP，可近似求解米勒平台电压 VGP 为：
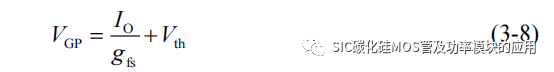
该阶段所对应 SiC MOSFET 的开通过程中的上升时间参数，可以求得该时间：
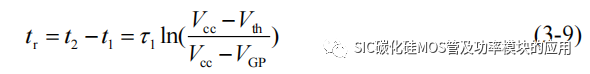
同时由于 SiC MOSFET 的 ids 上升，在回路寄生电感 LP 上会产生电压降，如图3-2 所示，当时 IDS=IO时，漏源极电压下降到 UDS0，此阶段的 uDS(t)可以表示为：
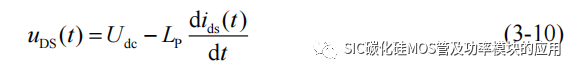
此阶段 SiC MOSFET 上的产生的开关损耗为：
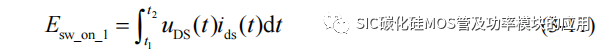
将(3-4)、(3-7)和(3-10)代入上式，即可求解第二阶段 SiC MOSFET 的开通损耗，得到近似结果为：
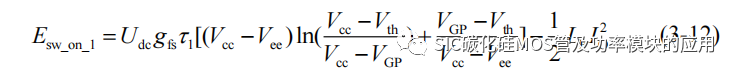
伴随着 SiC MOSFET 导通，上一个阶段进行续流的二极管 D1 会关断，因此产生二极管反向恢复损耗。
(3) t2-t3 阶段：t2 时刻栅源极电压进入米勒平台，此时 uGS(t)会出现一个小的电压下降，是由于 SiC MOSFET 导通后进入线性电阻区，输出电容 Coss的放电造成的，同时放电电流导致了 ids(t)达到电流尖峰 Ipeak，进入电流震荡阶段；uDS(t)下降至导通电压 UDS_on，可以表示为：
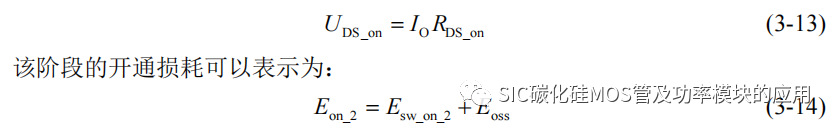
其中第一部分 Esw_on_2 为 SiC MOSFET 的漏源极电压下降导致的开通损耗，第二部分Eoss 为输出电容 Coss 的放电电流造成的沟道热损耗，根据能量守恒，认为 Coss 的存储的能量都转化为了沟道损耗，因此有：
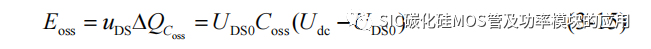
UDS0 可以根据 t2 和 uDS(t)的电压降求解，即：
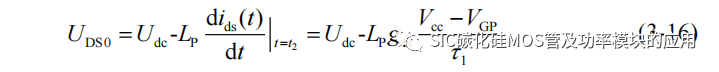
米勒平台阶段栅极电流主要为米勒电容进行充电，因此该阶段的维持时间可以
用漏源极电压的变化求得：
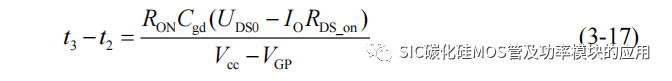
将漏源极电压 uDS 的下降曲线拟合为线性关系，此阶段的 SiC MOSFET 的开通损耗 Esw_on_2 可以估算为：
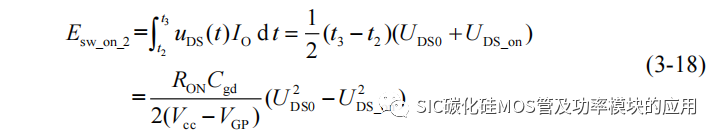
(4) t3-t4阶段：t3时刻开始 SiC MOSFET 已经饱和导通，其栅源极电压继续上升，直至 Vcc，从 t3 时刻开始，SiC MOSFET 的器件损耗由开通损耗转变为导通损耗。
以上为 SiC MOSFET 的开通过程的全部阶段，开通过程中的电路损耗主要由开通损耗以及续流二极管的导通损耗和反向恢复损耗构成。从 t0-t4，一个驱动周期内SiC MOSFET 的开通损耗 Esw_on 主要由 Esw_on_1 和 Esw_on_2 以及 Eoss 三部分组成，则一个驱动周期内的开通损耗功率定义为：
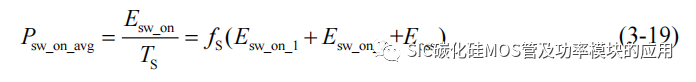
其中 TS 和 fS 分别表示驱动周期时间和驱动频率。
3.2.3 SiC MOSFET 关断损耗计算
如图 3-3 所示为基于 SiC MOSFET 的实际测试波形得的等效的关断过程电压电流波形示意图。为了简化计算，结合等效波形具体分析关断过程中各阶段的关断损耗和其他损耗。分析如下：
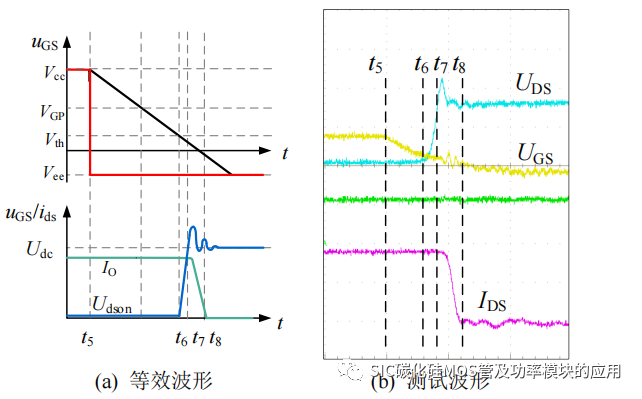
图 3-3 关断过程波形图
(1) t5-t6 阶段：t5 时刻开始，驱动器输出关断负电压，SiC MOSFET 开始进入预备关断过程，uGS(t)开始进入下降阶段，此阶段主要由 Cgs 和 Cgd 进行放电，因此可以将 uGS(t)近似表示为：
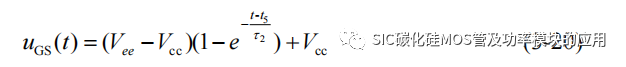
关断过程中的驱动回路总电阻为 ROFF，则关断过程时间常数 τ2 可以表示为：
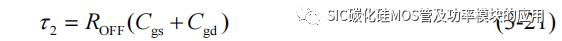
当 t6 时刻，栅源极电压 uGS(t)达到 Vth，下一时段 SiC MOSFET 将开始关断。t5-t6 阶段对应 SiC MOSFET 的关断延迟时间 td(off)，可以近似求解得到：
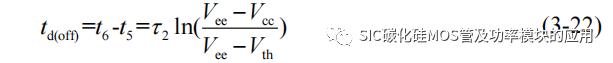
由于该阶段 SiC MOSFET 依旧处于饱和导通状态，因此该阶段产生的器件损耗以导通损耗为主。
(2) t6-t7 阶段：t6 时刻开始，uGS(t)下降低于 Vth，SiC MOSFET 开始关断，首先漏源极电压 uDS(t)开始近似线性上升，而漏源极电流 iDS(t)仍然保持输出电流 IO，此阶段 IO 开始为 SiC MOSFET 的输出电容充电，而根据上一节的分析，充电电流不再流经沟道，并不产生关断损耗，因此该阶段得关断损耗可以表示为：
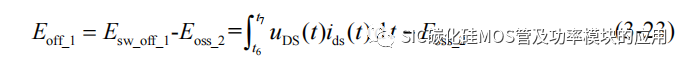
根据电容充电电流的表达式，可以近似表示该阶段的时间长度：
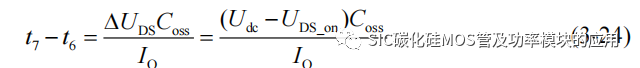
该阶段的输出电容的充电能量可以依靠电容的存储能量守恒来计算，即：
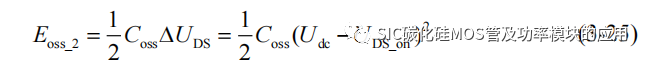
将(3-24)(3-25)代入(3-23)中，可以得到该阶段关断损耗为：
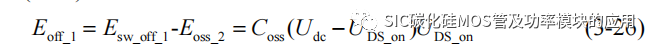
该阶段的 SiC MOSFET 以关断损耗为主，导通由于 SiC MOSFET 的沟道电流实际已经下降为 0，但是极间电容的充电电流会使漏源极 ids(t)仍维持在导通时刻的输出电流。
(3) t7-t8 阶段：t7 时刻开始，uDS(t)达到母线电压，因此 SiC MOSFET 的 ids(t）开始下降，而由于 ids(t)的变化，作用于寄生电感，产生关断瞬间的电压过冲。此阶段的关断损耗可以近似表示为：
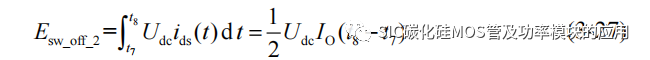
其中(t8-t7)对应 SiC MOSFET 器件手册中的下降时间 tf。
(4) t8-阶段：t8 时刻开始，SiC MOSFET 已经完全进入阻断状态，此时 SiCMOSFET 器件内沟道不再有电流流过，电路的输出电流开始由上管的体二极管 D1进行续流。
综上分析，一个开关周期内的关断损耗主要由 Eoff_1 和 Esw_off_2 两部分组成，可以得到周期内平均关断损耗功率为：
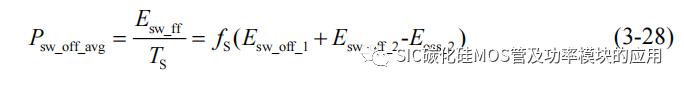
3.2.4 SiC MOSFET 导通损耗计算
SiC MOSFET 的导通损耗主要是由输出电流作用在导通后的沟道电阻上产生的热损耗，根据电阻的功率计算得到：
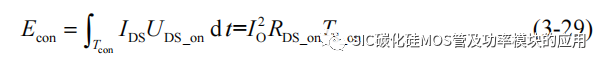
其中 D 为 SiC MOSFET 的驱动占空比，TS_on为一个驱动周期内的 SiC MOSFET的实际导通时间，可以依靠开关过程的导通、关断延迟和上升下降时间进行估算：
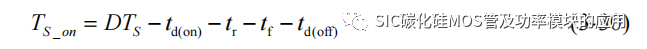
SiC MOSFET 的开通、关断过程持续时间相比于导通时间可以忽略，因此可以近似认为导通损耗产生时间为导通时间。
3.2.5 其他损耗计算
3.2.5.1 驱动损耗
SiC MOSFET 的驱动损耗产生的主要原因是为保证器件有效开通，使 uGS(t)的电压能够达到有效开通电压所需要的充电电荷 QG 消耗的能量。QG 是表征 SiCMOSFET 的有效驱动电流和开通延迟时间关系的特征量。如图 3-4 所示，为C3M0075120K 手册[79]中给出的栅极电荷和栅源极电压曲线，该曲线表征为达到不同栅源极电压时所需要的充电电荷。基于该曲线可以近似估计SiC MOSFET 导通过程所需要的充电电荷，进一步估算栅极电荷所消耗的损耗。
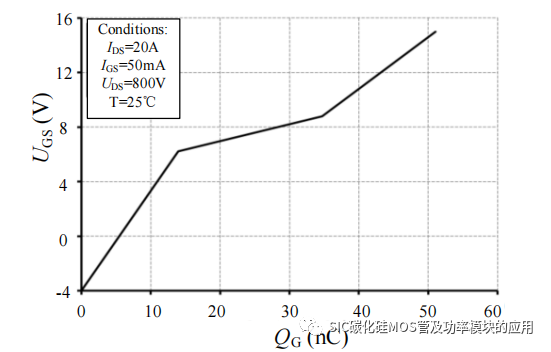
图 3-4 栅源极电压和栅极电荷曲线
栅极驱动损耗功率可以用下式进行估算为：
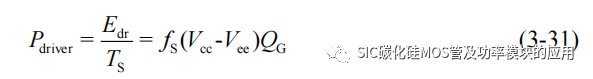
3.2.5.2 二极管导通损耗
由于一个开关周期，SiC MOSFET 仅导通 DTS 的时间，关断时电路的输出电流流过上管的体二极管 D1 进行续流，而 SiC MOSFET 的体二极管也存在导通电阻，因此也会产生相应的二极管导通损耗 Econ_FD：
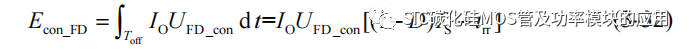
其中 UFD_con 为体二极管的正向导通电压，trr 为二极管的反向恢复时间。一个开关周期内的二极管导通损耗功率为：
3.2.5.3 二极管反向恢复损耗
当二极管由导通状态转变为截止状态，二极管上会瞬间出现一个反向电流，反向电流逐渐减小为 0，随后二极管才完全进入关断状态。反向恢复电流的产生主要是由二极管的电荷的存储效应导致，当二极管施加正向电压时，二极管内的电子和空穴扩散，导致了在导通期间的大量存储，当二极管施加反向电压后，存储的电子和空穴将会反向移动，从而在存储电荷消耗尽前，二极管仍处在 PN 结正偏的状态，因此会产生反向恢复电流。从反向恢复电流出现到恢复所用的时间定义为二极管的反向恢复时间 trr，二极管反向恢复过程中产生的损耗为：
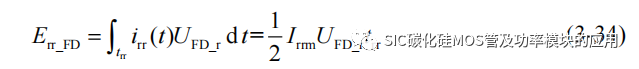
式中 UFD_r 为二极管反向关断后承受的反向电压，Irrm 为二极管的反向恢复电流的峰值。在 Boost 电路中，其关断后的反向关断电压为：
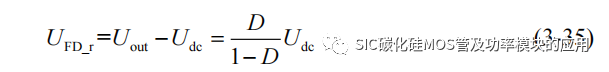
可以进一步得到一个开关周期内的二极管反向恢复损耗功率为：
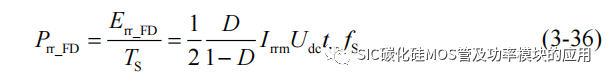
而 SiC MOSFET 器件寄生二极管表现为肖特基二极管特性，相比于传统 Si 二
极管，SiC 肖特基二极管的反向电流很小，可以忽略不计。
基于上述分析，可以得到一个开关周期内 SiC MOSFET 的器件损耗功率为：
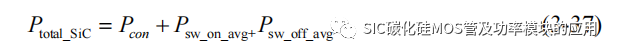
3.3 SiC MOSFET 温度特性分析
SiC MOSFET 的内部电子迁移率 μ 可以表示为一个关于温度 T的函数：
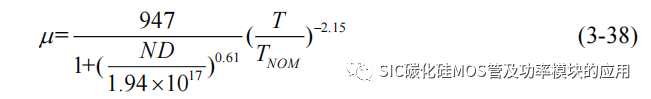
式中 ND 为漂移区的掺杂，T 表示标称结温，TNOM 温度标称温度参考。SiC MOSFET 器件呈现正温度特性，其沟道电流是关于 μ 的函数，从式(3-38)来看，μ 是一个负温度特性的参数，由于 SiC MOSFET 内部分晶格散射作用导致了温度升高后有效电子迁移率的降低。
阈值电压 Vth 是 SiC MOSFET 器件自身的本征参数，是由器件内部介电常数、本征载流子浓度、空穴浓度和器件温度等特性参数决定的[77]；导通电阻 RDS_on 是当SiC MOSFET 饱和导通后的等效电阻，会受到漏源极电压、电流的限制，而这两项特性参数都是由具有负温度特性的电子迁移率所决定的，因此导通电阻是具有正温度特性参数。如图 3-5 所示，为 CREE C3M0075120K 手册[79]中给出阈值电压和导通电阻随温度变化的曲线。
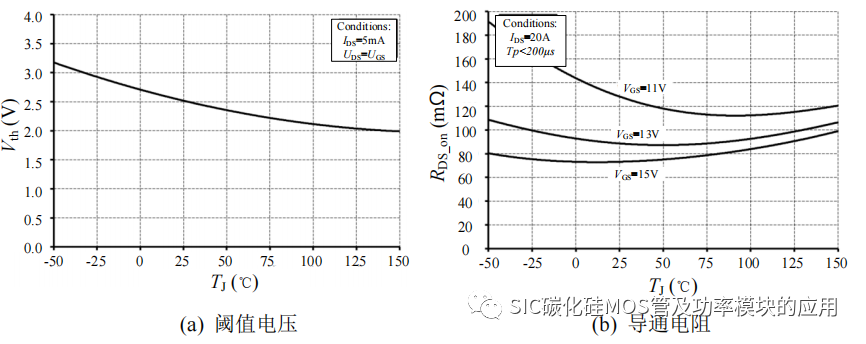
图 3-5 SiC MOSFET 随温度变化曲线
SiC MOSFET 的温升是由于自身的器件损耗以热量的形式已进行释放，造成节温升高，而阈值电压和导通电阻的变化无论是对于并联 SiC MOSFET 的均流效果还是对于开通关断损耗都会产生影响。
3.3.1 温度对于并联 SiC MOSFET 均流影响分析
(1) 阈值电压 Vth：第三章已经分析当阈值电压不均衡造成的动态均流差异，Vth是随温度上升而降低，SiC MOSFET 的温度主要受到导通损耗影响，当并联支路电流存在差异，支路电流大的，导通损耗大，导致的器件温升更高，阈值电压随之减小，开通延迟降低，关断延迟增加，造成导通时间的增加。因此温升对于并联 SiCMOSFET 的动态均流不平衡度也呈现正温度特性。可以根据(3-6)和(3-22)近似求解开通和关断延迟时间，由延迟时间造成的导通时间差异对于温度的偏导数：
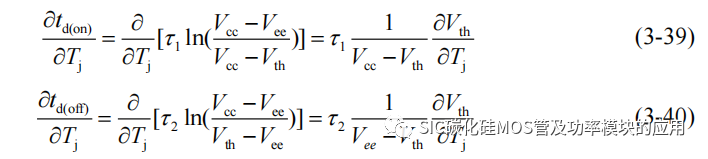
根据(3-39)和(3-40)可知开通延迟对温度的偏导是负数，关断延迟对温度的偏导是正数，导通时间差异整体对温度呈现正温度特性，因此温度差异会加剧动态均流差异。
(2) 导通电阻 RDS_on：导通电阻的影响主要体现在 SiC MOSFET 的饱和导通阶段，此时 SiC MOSFET 等效为低阻值电阻，导通电阻将直接决定流过并联支路的电流大小。从图 3-5 可以看出，导通电阻在室温及以上温度时，呈现正温度特性，理论上对于静态均流有利，可以构成负反馈促进并联均流。具体工作等效流程如图 3-6 所示，只要在静态均流阶段存在均流不平衡，则导致电流大的导通损耗更高，造成更高的温升，从而使导通电阻变大，降低电流不均衡度，直至达到电流平衡。
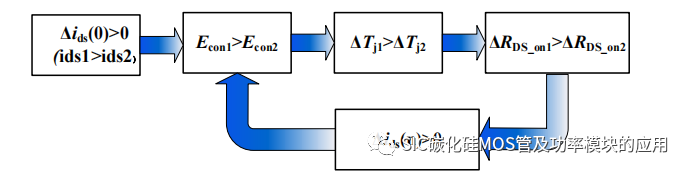
图 3-6 温度对静态均流影响反馈过程示意图
基于第二章的图 2-8 可以推导得到静态均流过程中的电流的表达式，假设 i1 和i2 表示并联的两个 SiC MOSFET 的电流，且有 i1=i2+Δi，则导通电阻 RDS_on1<RDS_on2并且有回路寄生电感 LP1<LP2，并联电流可以写为：
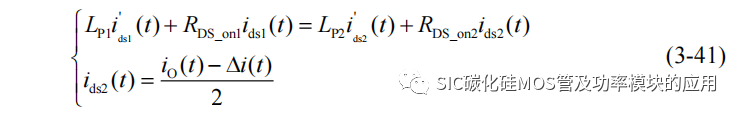
SiC MOSFET 导通期间母线电压 Udc 为 L 充电，则输出电流 iO(t)可以看作为斜率为 Udc/L 的线性方程；由上一章的分析知由寄生电感差异引起的静态均流过程中的不平衡电流是一个短时间内趋于稳定的值，因此近似认为 Δi’(t)为 0，可以得到 Δi的近似表达式：
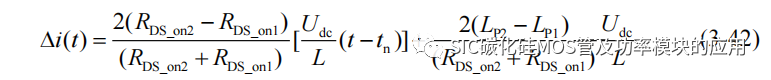
上式中的 tn 表示第 n 个驱动周期的导通起始时间。进一步对上式求偏导，可以得到：
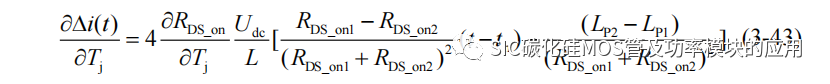
RDS_on1<RDS_on2，所以上式静态电流差异对温度的偏导数为负值，所以静态均流差异是具有负温度特性，温度的提升将有助于实现静态均流。
3.3.2 温度对 SiC MOSFET 损耗影响分析
SiC MOSFET 的阈值电压 Vth 和导通电阻 RDS_on 都是关于温度的函数，在开关损耗过程中 Vth 决定 SiC MOSFET 的导通时间，RDS_on 随温度升高而升高，将会造成导通损耗的增加。为进一步分析结温 Tj对 SiC MOSFET 各阶段损耗的影响，基于图 3-5 中阈值电压随结温变化的特性曲线，截取特征值点，进行二次项拟合，近似得到 Vth(Tj)，如
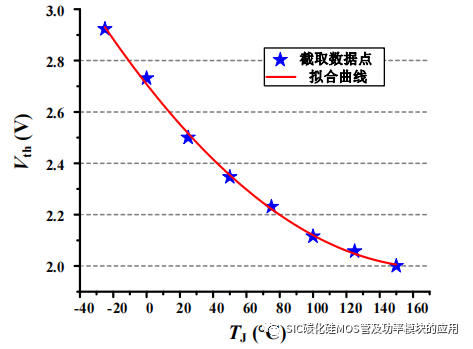
图 3-7 所示为截取的特征值点和拟合得到的函数曲线。
得到的阈值电压 Vth(Tj)的拟合方程为：
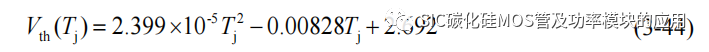
导通电阻 RDS_on 进行拟合，可以得到相应的导通电阻温度函数 RDS_on(Tj)：
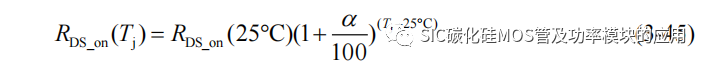
SiC MOSFET 的一个导通周期内，由于 SiC 器件特性，开通关断时间短，因此得一个周期内得器件损耗以导通损耗为主，损耗产生的焦耳热导致 SiC MOSFET 器件结温升高，导致导通电阻随着结温变化，造成导通损耗的增加。进一步分析导通损耗的温度变化规律。由于温度升高导致 SiC MOSFET 阈值电压下降，根据(3-39)和(3-40)可以估算出导通损耗增加时间，导通损耗温度函数为：
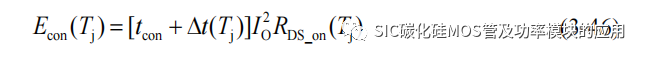
其中 Δt(Tj)是由于 SiC MOSFET 结温上升导致的缩短的开通延迟时间和增加的关断延迟时间，可以依靠阈值电压近似求解：
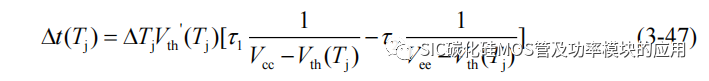
此外导通电阻也是随结温正向变化的函数，结温上升，导通电阻增加，所以温度的上升将会加剧 SiC MOSFET 器件导通损耗。但是电力电子器件在实际应用中会加装散热装置，以限制 SiC MOSFET 结温上升，假设金属散热器和 SiC MOSFET 直接连接，则 SiC MOSFET 和散热器之间的热平衡方程为：
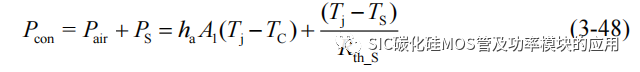
式中Pair为SiC MOSFET和空气之间的热量传递，Ps为与散热器之间的热传递功率，ha 为空气的自然换流系数，A1 为 SiC MOSFET 和空气的有效接触面积，TC 为环境温度，TS 为散热器温度，Rth_S 为散热器的等效热阻，其定义为：
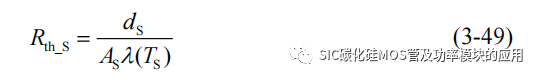
热阻是一个关于散热器本身导热系数 λ 和器件厚度 dS 以及有效接触面积 AS 的变量。由于散热器的导热系数相比于空气更大，因此可以将 SiC MOSFET 的散热功率等效为与散热器之间的热量传递。只有当 SiC MOSFET 的热损耗功率和 Ps 之间达到热平衡，才会产生达到稳定结温。而热平衡达到的稳定结温将会限制导通电阻正温度特性辅助实现并联自均流的均流范围。
3.3.3 温度对于 SiC MOSFET 并联损耗影响分析
SiC MOSFET 的器件特性决定了 SiC MOSFET 的损耗特性相比于 Si IGBT 要更好，开通关断时间更短，有效地降低开关损耗，更低的导通电阻，相同输出电流等级下的导通损耗更低。SiC MOSFET 的并联结构下，可以实现系统的容量提升，而且在导通过程中导通电阻相比于单 SiC MOSFET 小了近一倍。具体两种方式下的导通损耗可以表示为：
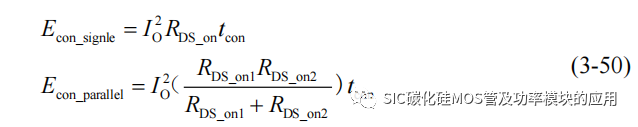
由上式可知，在输出电流恒定的条件下，只有当导通电阻相等时，实现并联 SiC的导通损耗的最小化。当并联 SiC MOSFET 的支路电流，会由于寄生电感的不平衡产生静态均流不平衡，假设并联支路电流有 I1>I2，根据并联电压平衡方程有：
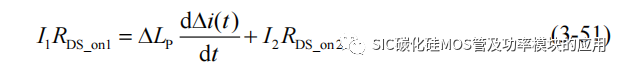
将由于静态均流差异会在导通时间内趋于稳定，因此上式可以近似表达为：
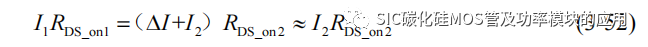
为简化分析可以将寄生电感的差异近似等效为导通电阻的差异造成。而开通过程 SiC MOSFET 的导通损耗将转化为器件的热量，造成的温升导致导通电阻的变化视为离散迭代过程，假设并联的 SiC MOSFET 的通过散热器进行的热传递相同，且每一个周期的导通损耗有 KS 的部分转变为 SiC MOSFET 结温，且并联的器件的热阻 Rth 相同，则每个 SiC 经历一个周期的导通损耗后的温升和下一个周期导通开始时的导通电阻为：
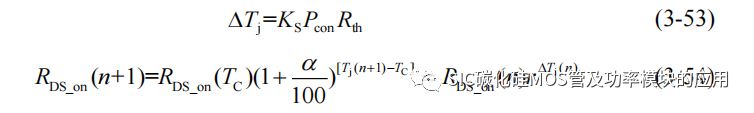
其中 r 为导通电阻系数，RDS_on(n)表示第 n 个驱动周期的导通电阻，假设输出电流为 IO恒定，一个导通周期的电流可以用导通电阻近似计算，进而可以将第 n 个周期的导通损耗可以表示为：
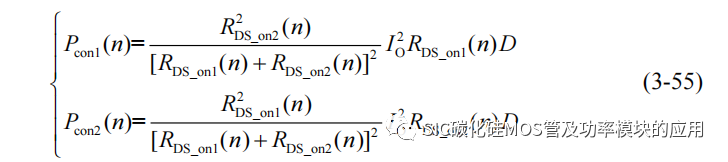
同时可以计算第 n+1 个开关周期的导通电阻为：
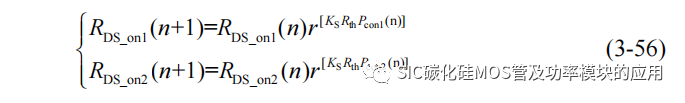
为直观描述并联 SiC MOSFET 的温度，导通电阻和导通损耗变化趋势，在MATLAB 软件中绘制温度和导通损耗曲线。相关参数参考于 C3M0075120K 手册，输出电流为 20A，根据手册中的导通电阻–温度曲线，拟合出导通电阻系数 r 为 1.011，设每个开关周期 SiC MOSFET 导通占空比 D 为 0.5，热阻 Rth 设置为 1.1℃/W，导通损耗转化率 KS 为 0.1。
假设由于寄生电感导致并联电流存在 1.2A 的差异，等效到导通电阻差异10mΩ，则等效初始电阻分别为 75mΩ 和 85mΩ，得到导通电阻、导通功率变化趋势曲线如图 3-8 所示，其中横坐标表示第 n 个驱动开关周期。从图 3-8 中可以看出，随着开关周期的增加，导通电阻和并联电流趋于一致，这与上一节中温度对并联静态均流具有促进作用的结论相符合。但随着温度的提升，导通损耗随着导通电阻的增加和温度的提升而变大，并联 SiC MOSFET 损耗的功率变化趋势为朝向功率均衡分配发展，但整体损耗继续提升。如果没有有效的散热功率，或超过热平衡条件，将会造成并联 SiC MOSFET 的热损坏。实际中 KS 并非恒定系数，是受到散热功率系统的功率影响的，当 KS=0 时，则系统实现热平衡状态，结温不再发生变化。
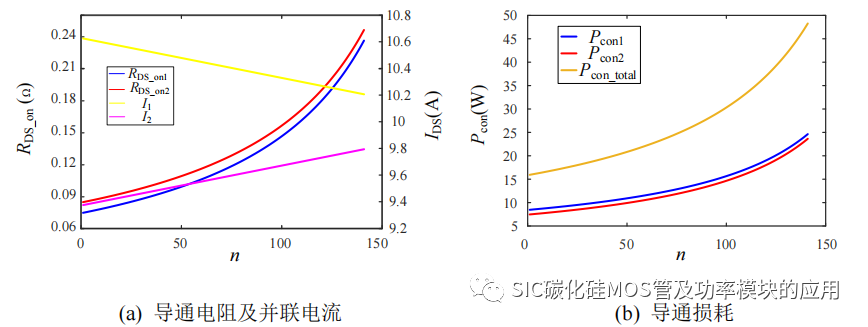
图 3-8 并联 SiC MOSFET 导通电阻及导通损耗变化趋势
在电力电子功率电路中，会加入散热系统，散热功率和器件损耗之间的传导率将决定其温度和损耗的变化趋势，为进一步说明损耗和稳态温度的关系，给出如图3-9 所示的器件损耗和的散热功率热平衡示意图，其中黑色曲线代表随温度变化下的 SiC MOSFET 的器件损耗 PSiC，蓝色曲线表示散热功率随温度变化趋势，①、②、③分别表示散热能力由强变弱的三种散热功率等级情况。
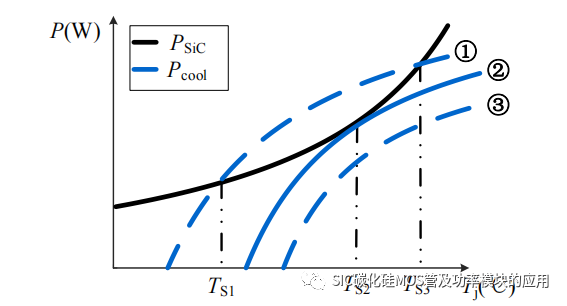
图 3-9 器件损耗和散热损耗随温度变化曲线
图中 Pcool的温度曲线和 PSiC 之间的交点为系统的热平衡温度，此后器件损耗和散热功率都不再变化，器件结温变为稳态值。当 PSiC>Pcool时，Tj 将会继续上升直至热平衡温度，此状态下 KS>0，并联 SiC MOSFET 具有自均流条件；当 PSiC<Pcool时，Tj 开始回降至稳态温度，KS=0，并联自均流条件被破坏；当③种情况发生，保持PSiC>Pcool，Tj 持续上升，最后 SiC MOSFET 发生热失效。
3.4 SiC MOSFET 损耗仿真
为了进一步研究 SiC MOSFET 的损耗关系，在 PLECS 软件中，利用 CREE公司提供的 C3M0075120K 器件模型进行损耗分析，仿真主要是模拟对比不同场景下的 SiC MOSFET 的电流损耗变化，以及并联 SiC MOSFET 温度不平衡、导通电阻不平衡条件下的损耗比对。首先搭建基于 SiC MOSFET 的 Boost 升压电路模型，模型的输入电压为 100V，输出电压为 200V，负载电流 20A，其中 SiC MOSFET 的驱动信号由 2kHz 变化到50kHz，SiC MOSFET 的模型参数来自于 CREE 公司，其中 Boost 续流回路的二极管采用 C3M0075120K 的体二极管模型，来模拟 SiC MOSFET 半桥模块的应用。记录 SiC MOSFET 的开通损耗、关断损耗和导通损耗。
3.4.1 单管 SiC 和并联 SiC MOSFET 损耗仿真
首先对比单管 SiC MOSFE 和并联 SiC MOSFET 下相同输出电流，损耗差异，仿真中的 SiC MOSFET 的起始导通电阻为 75mΩ，初始温度为 25℃，仿真模型中加如等效热阻抗，得到稳定后的 SiC MOSFET 的导通损耗，开通、关断损耗及体二极管续流器件的导通损耗数据，对比单 SiC MOSFET 损耗和并联损耗如图 3-10 所示。其中图中Ⅰ为单管 SiC MOSFET 的相关损耗，Ⅱ为并联 SiC MOSFET 结构下的损耗功率大小，图中显示的是并联两个 SiC MOSFET 的总损耗功率。图 3-11 所示为不同频率下两种电路结构的系统效率。
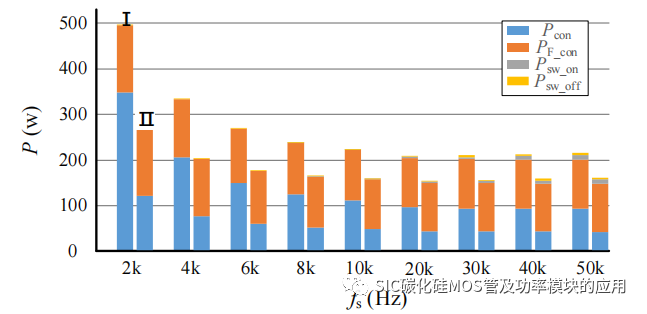
图 3-10 不同频率下 SiC MOSFET 损耗仿真结果
对比图 3-10 中的损耗，并联 SiC MOSFET 的导通损耗和开关损耗相比于单管SiC 有所下降，但是由于输出电流一定，因此二极管的导通损耗基本无变化；而低频率下的开关损耗较低，当频率提升后，导通损耗功率开始下降，但开关损耗提升，因此系统的效率会达到一个最高效率后，由于开关损耗功率的提升而出现下滑，如图 3-11 中两种情况下效率都具有相同的趋势。
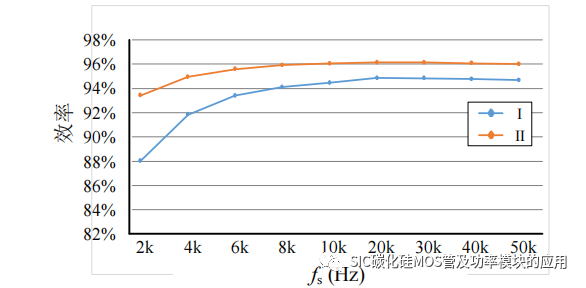图 3-11 两种结构下电路效率变化曲线
3.4.2 SiC MOSFET 温度提升对损耗影响
为验证 SiC MOSFET 的结温对并联损耗的影响，在 SiC MOSFET 的并联电流均衡的条件下，改变其中一个 SiC MOSFET 所连接的散热基板的恒温源温度，从而改变稳态达到热平衡后 SiC MOSFET 的结温。并且 SiC MOSFET 的初始温度都是25℃。由于 PLECS 软件中对于 SiC MOSFET 的模型中没有对应导通电阻温度函数，因此仿真结果直接体现损耗和温度之间的关系。
如图 3-12 所示，为并联 SiC MOSFET 在连接不同温度的恒温源下的器件损耗。从图中可以看出随着恒温源的温度的提升，SiC MOSFET 的开关损耗和导通损耗都略有增加。当并联支路电流相同的情况下，温度高导通电阻会略有增加，因此直接造成导通损耗的增长。由于散热基板和散热源之间的热阻恒定，可以看作系统的热平衡状态下的损耗和散热传导功率相同，导通损耗的增加直观的反映出导通电随热平衡状态下的变化量。
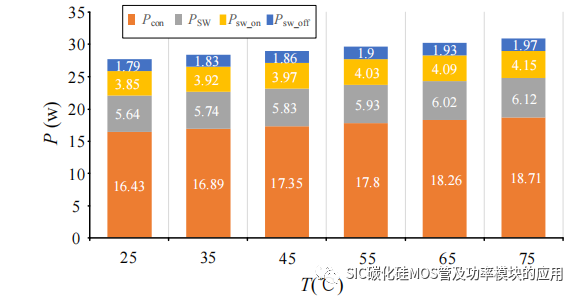图 3-12 不同温度下 SiC MOSFET 器件损耗
3.4.3 SiC MOSFET 并联电流不均衡对损耗影响
根据第二章的分析，寄生电感对静态均流的影响在导通阶段，当寄生电感量固定后，静态均流差异在导通周期内等效为一个稳态量，因此可以将寄生电感导致的均流差异等效为导通电阻差异，来模拟寄生电感量的差异。仿真结果如图 3-13 所示，其中Ⅰ表示 SiC MOSFET1，逐渐增加其到导通电阻来对应并联支路寄生电感的增加，Ⅱ表示 SiC MOSFET2，其导通电阻不变。其中图 3-13(a)为不同静态均流差异下的损耗变化散热条件一致，静态均流差异将加剧功率不均衡分配，支路电流越大对应损耗越大且热平衡下的结温越高。
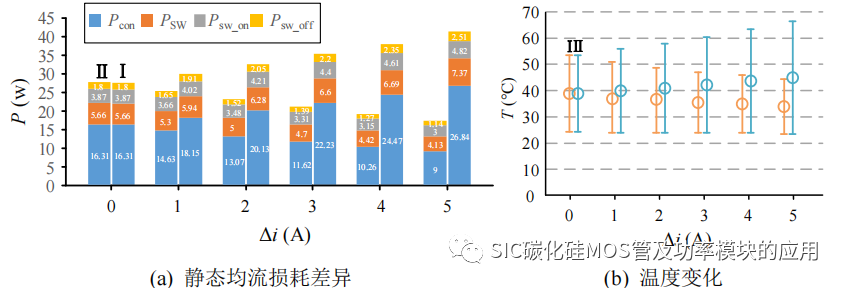图 3-13 静态均流不平衡对损耗和结温的影响
为进一步验证静态均流不平衡对到导通电阻、温度以及损耗的影响，在 SiCMOSFET 模型中加入导通电阻温度函数，进行静态电流不均衡下的热平衡仿真。设定并联的 SiC MOSFET 共用一个散热平台，经过 0.18 的热阻热容模块连接 25℃的恒温源，实现有效散热，SiC MOSFET1 的导通电阻为 75mΩ，SiC MOSFET2 设定为 100mΩ 以产生约 2A 的静态均流差异。得到并联均流波形、导通电阻、结温和导通损耗变化波形，如图 3-14 所示。从仿真结果来看，初始存在大约 1.2A 的静态均流差异，因此 SiC MOSFET1 的结温上升更高，导致导通电阻增加，从而静态电流差异开始减小，但是并联的两个SiC MOSFET 都会伴随导通损耗的产生而结温上升，从而造成导通电阻的增加，只是 SiC MOSFET1 的导通电阻增加量更大，因此会朝向均流发展，当系统达到热平衡后，SiC MOSFET 的损耗和结温到稳定，SiC MOSFET 并联均流稳定。因此 SiC MOSFET 的自均流特性受到环境温度，热阻和导通损耗的限制，SiC MOSFET 可以在一定范围的不均衡电流差异内实现自均流。
此时的仿真模拟图 3-9 中①的情况，开始 SiC MOSFET 的器件损耗大于散热功率，造成 Tj 上升从而满足并联自均流的条件，电流出现均衡化，但是当 Tj 达到稳态温度后，不在变化，自均流也受到了限制。为了进一步说明并联 SiC MOSFET 的自均流局限性，考虑器件损耗和散热功率之间的关系，对图 3-9 的③极端状态进行模拟，得到的结果如图 3-15 所示。仿真为了模拟散热功率不足，去除散热基板所连接的恒温源，并联 SiC MOSFET 之间依靠基板直接连接，进行热传导，加速温度提升。可以看到 2s 内电流朝向自均流发展，但是由于缺乏有效散热，在 3s 后，SiC MOSFET电流开始迅速提升发生热击穿，而且 3s 时发生热击穿时，并联均流未实现完全的静态均流。所以综合仿真结果，SiC MOSFET 具有正温度特性，有利于并联电流的均衡发展，但自均流能力受到散热条件影响，存在局限性。
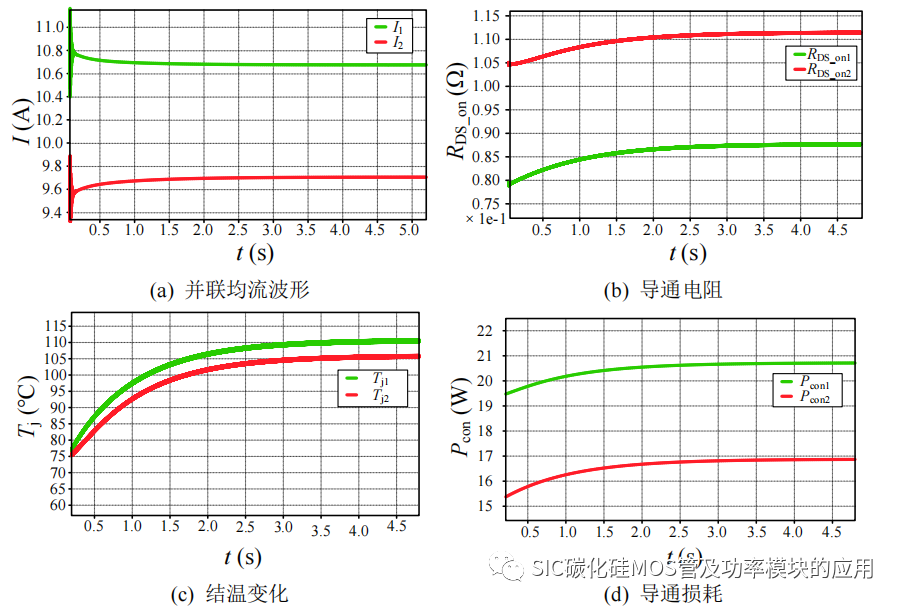
图 3-14 并联均流不平衡下仿真
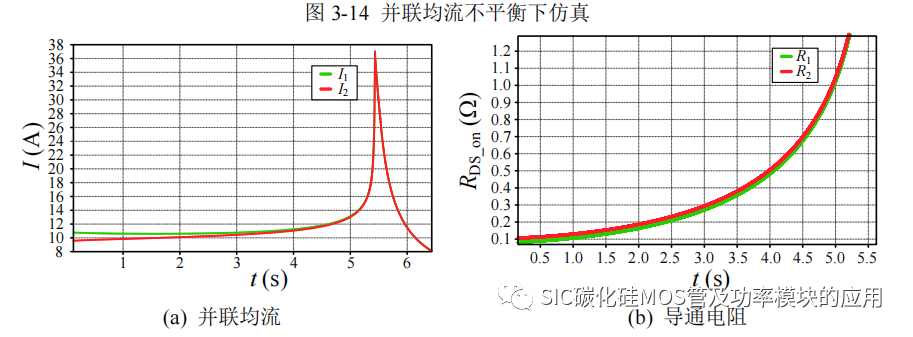图 3-15 极端条件下自均流仿真
3.5 本章小结
本章首先结合 SiC MOSFET 的参数模型和开通关断过程对器件损耗进行了推导，然后结合所推得的损耗公式针对 SiC MOSFET 的结温影响进行了分析，表明当并联 SiC MOSFET 存在并联电流不均衡情况下，导致的结温差异，对于 SiC MOSFET的静态均流具有促进作用；之后进一步分析了结温变化和并联损耗分配之间的关系，并针对上述分析，在 PLECS 仿真模型中搭建基于 SiC MOSFET 的 Boost 电路热仿真模型，对上述分析进行了验证，也验证了 SiC MOSFET 并联自均流的局限性。
第 4 章 SiC MOSFET 串联驱动设计
4.1 引言
由于 SiC MOSFET 在串联结构中，相互串联的 SiC MOSFET 的源极和上管的漏极相连，因此串联 SiC MOSFET 将会均分母线电压，此时的 SiC MOSFET 源极相对于驱动控制电路的地为悬浮高压状态，需要特别注意 SiC MOSFET 的功率源极和低压控制回路之间的电气隔离，目前市场上商业化的 SiC MOSFET 驱动 IC 多采用变压器磁隔离技术，可以达到 2kV 的最大电气绝缘限度。但是串联的 SiC MOSFET要实现串联均压首先要保证驱动信号的实时同步性，实现开通关断的一致，采用驱动 IC，每一个芯片之间不存在耦合，无法实现输出驱动电压的同步性，本章结合 SiCMOSFET 隔离型驱动电路基本电路提出了一种适用于 SiC MOSFET 串联结构的变压器隔离型驱动电路，本章节具体分析了驱动电路原理及开关过程，介绍了相关器件设计，并结合仿真软件进一步验证了驱动器的可行性。
4.2 变压器隔离式串联驱动分析
如图 4-1 所示文本文所提的一种适用于串联 SiC MOSFET 结构的驱动电路原理图。左侧为 S1 构成的正激功率转换电路，将串联驱动信号转变功率电压信号,经过脉冲变压器后的电压能够满足驱动要求。次级变压器后级接入推挽结构和储能电容将驱动电压信号进行二次电流提升，为 SiC MOSFET 提供充足驱动电流。
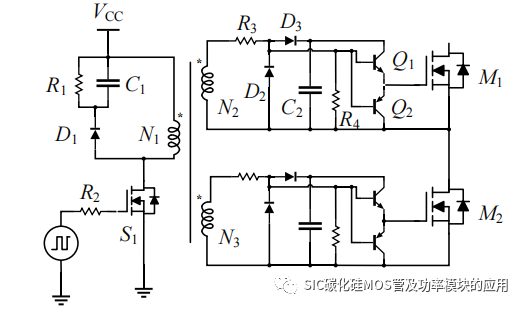
图 4-1 变压器隔离型串联驱动电路
驱动信号经过正激变换器进行电压功率放大，针对正激变换器的特点，为防止变压器线圈磁饱和，加入由 R1、C1、D1 构成的 RCD 吸收电路，在驱动信号为低时，S1 关断，原边绕组 N1通过 RCD 吸收电路将存储的能量进行消耗，防止磁饱和，此外在副边绕组中加入 D2、R3 构成的泄放回路辅助去磁。M1 和 M2 为串联的 SiCMOSFET，N1、N2、N3 构成串联 SiC MOSFET 的隔离变压器绕组，其匝数比为 1:1:1；R3 还起到限制变压器绕组震荡的作用，且在去磁过程中限制电流变化；C2 为储能电容，保证驱动瞬间 SiC MOSFET 所需的电流。R4 为下拉电阻，为后级 Q1、Q2 组成的推挽电路提供导通条件。
由于串联驱动需要保证驱动信号的一致性，因此所提出的针对串联 SiCMOSFET 的变压器隔离型驱动电路的每个驱动支路采用完全相同的电路结构和器件参数，分析驱动电路过程针对其中一个 SiC MOSFET 的驱动电路进行分析，其开关过程栅极电流回路和原边绕组电流回路如图 4-2 所示。开通关断过程的次级电感电压、电流及输出驱动电压典型等效波形如图 4-3 所示。该串联驱动电路的具体开关过程分析如下：
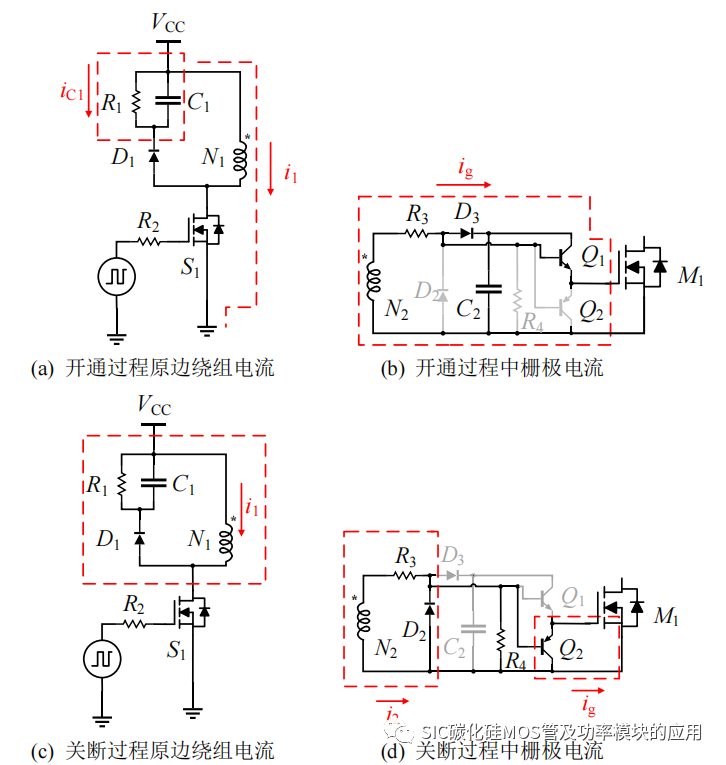图 4-2 开关过程电流回路
图 4-3 中 Vg 表示对 S1 施加的驱动信号；UN1 表示原边绕组的电压；UC1 表示RCD 吸收电路中电容电压；UGS 表示驱动电路输的 SiC MOSFET 驱动电压；IN2 和IC2 分别表示变压器次级绕组 N2 输出电流和储能电容 C2 的输出电流。(t0-t1)阶段：t0 时刻，Vg转变逻辑高电平信号，S1 开始导通，此时驱动电源 VCC开始对 N1 充电，绕组 N1 和 N2 的同名端都为正，二极管 D3 导通，D2 截止，N2 等效为电压源输出接近 VCC 的电压值，为 C2 开始充电，Q1、Q2 的基极为正电压，Q1 导通、Q2 截止，栅极充电电流提供回路，串联的 SiC MOSFET 的栅源极驱动电压开始同步上升，SiC MOSFET 开始导通。由于 SiC MOSFET 是电压型器件，因此栅极电流主要是对栅源极电容 Cgs 充电和消除栅极电荷导致的，因此 IN2 的电流会开通瞬间产生一个较大电流尖峰，同时 C2 辅助变压提供驱动电流，SiC MOSFET 导通后，驱动电压维持在正电压，并不消耗电流，IN2 和 IC2 维持在零电流。在 SiC MOSFET 导通期间，由于二极管 D3 的压降，所以驱动正向电压略低于 VCC。
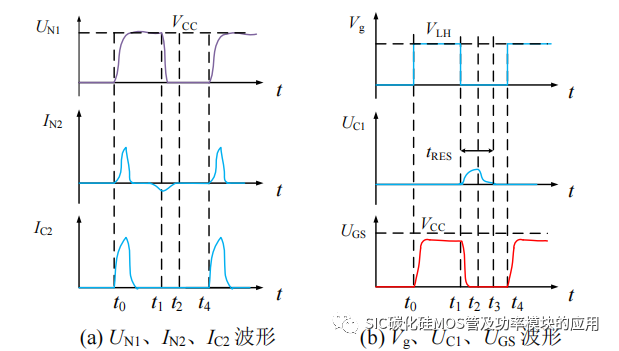图 4-3 串联驱动开通关断过程等效波形图
(t1-t3)阶段：t1 时刻，驱动逻辑信号 Vg由导通信号转变为截止信号，S1 关断,此时原边绕组 N1 会继续维持电流，但是变压器同名端等效为负压，N2 的电流反向，D2 导通，D3 截至；变压器同名端等效电压反向，因此下拉电阻 R4 两端的电位反向，Q1 和 Q2 的基极电位低于驱动正电压，Q1 截至，Q2 开始导通，驱动栅极电流经过 Q2开始泄放，驱动栅源极电压下降。存储在 N2中的能量经过 D2 和 R3进行去磁。由于原边绕组也经过 RCD 吸收同步进行电能消耗，因此相比于开通时刻尖锋电流，关断时的 IN2 较短的时间反向流过，便随着去磁结束而变为 0。同时在该阶段，由于加入 RCD 吸收电路为变压器去磁，在 S1 关断后，有 N1 经过 D1 为 C1 充电，同 R1消耗消耗 N1 存储的能量，所以 t1 到 t2 阶段，C1 的电压上升，当达到最大值时，有 C1 电压加上 D1 的导通压降等于 N1 的电压，C1和 N1 之间近似发生谐振，t2 时刻开始 C1 的电压下降，R1 消耗 C1 的储能。(t3-t4)阶段：t3 时刻开始变压器复位，栅极电压维持在零电压，直到 t4时刻下一个周期的驱动信号的上升沿的到来，开始重复上述过程。
4.3 串联驱动电路相关设计
4.3.1 SiC MOSFET 驱动计算
为了保证 SiC MOSFET 有效地实现导通和关断状态地维持，需要针对驱动电路相关器件参数进行有效的设计，确保驱动电路能够输出充足的驱动功率，驱动电流，保证驱动电压在有效范围内。
(1) 驱动功率：SiC MOSFET 的开通过程中需要克服寄生电容，来保证栅源极电压的提升；而在开通关断过程栅极电流回路的电阻产生驱动损耗，因此驱动电路需要大于驱动损耗，根据上一章中对驱动损耗的估算公式(3-31)和为消除 SiC MOSFET 开通过程震荡而放置的栅极辅助电容 CGS，可以得到 SiC MOSFET 的最小驱动功率：
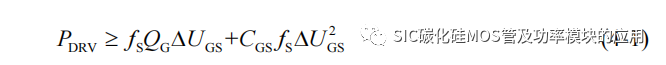
以 CREE 的 C3M0075120K 为例，驱动电压为 15V/-4V，充电电荷为 51nC,在50kHz 的驱动频率下，驱动栅极辅助电容 2.3nF，则单个 SiC MOSFET 所需驱动功率为：
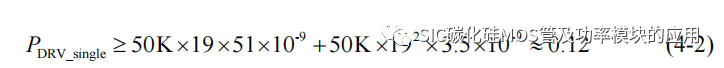
(2) 驱动峰值电流：考虑驱动回路中的等效寄生电感 Lg时，可以得到栅极驱动电流回路方程为：
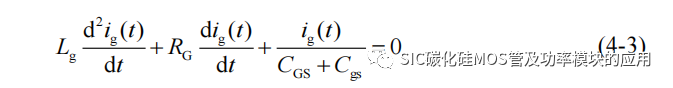
由于方程是一个二阶系统，其临界阻尼条件为：
当驱动电阻大于该值时，栅极电流处在过阻尼状态，不会发生震荡，在此条件下可以求计算得到驱动可以达到的最大峰值电流：
上式求解得到是在临界阻尼条件下的驱动电流的最大值，实际设计中，往往加大栅极电阻，确保驱动的回路电流处于欠阻尼状态下，因此设计、计算时需要乘以一个衰减因此，来确定最大电流。
4.3.2 RCD 缓冲电路计算
结合图 4-3 进行 RCD 缓冲电路参数设计，从 t0 时刻开始，原边绕组开始充电，绕组等效的线圈电感 LM 的电流持续上升，到 t1 时刻充电结束，LM 电流达到最大值，根据电感电流关系可以得到 t1 时刻峰值电流近似为：
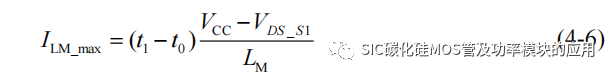
在驱动为低电平的阶段，即从 t1 时刻开始，LM 可以等效为 ILM_max 的电流源对C1 进行充电，此阶段若忽略二极管导通压降，可以等效视为 LC 发生并联谐振，谐振持续时间受 RC 取值影响，也和输入电压相关，假设 RC 取值较合适，可以根据谐振频率对持续时间进行估算：
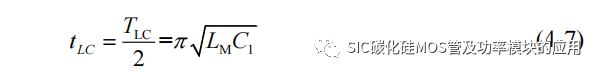
在谐振阶段，电感能量主要为电容充电，根据能量守恒关系有：
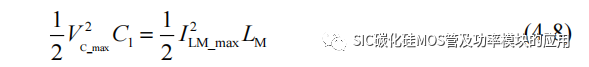
可以进一步计算谐振结束时的 C1 最大电压：
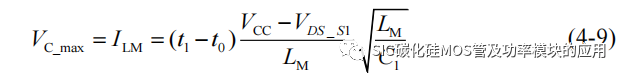
此后 C1 的电压经过 R1 开始释放，因此该阶段持续时间主要 RC 串联回路时间常数 τ 来决定，通常取 5 倍的 τ 视为电容电压接近于 0V。因此可以得到变压器去磁时间：
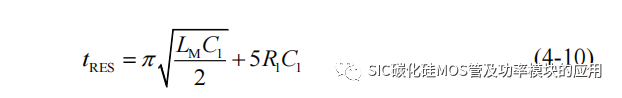
为了防止去磁不完全，需要去磁时间小于关断时间，因此有：
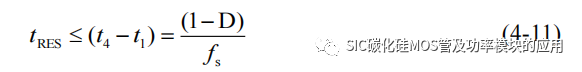
RCD 的参数选择极为重要，在确定 R1 和 C1时需要根据实际最高开关频率和最大占空比进行计算和选择，保证每一个周期内都能达到有效去磁，防止变压器的磁饱和的出现，导致变压器失效，串联驱动电路无法工作，可能造成 SiC MOSFET 烧毁。实际选取根基需要设定的去磁时间，去磁 RCD 结合上式进行计算。
4.3.3 驱动变压器计算
因为驱动信号的开关频率较高，驱动功率较低，所以变压器的体积将会大大缩小。变压器的设计可以采用面积乘积法进行简单估算，首先需要根据 SiC MOSFET的驱动功率和串联个数决定变压器的传输功率。其次根据变压器的功率和开关频率，进一步求解变压器磁芯所需窗口面积，即计算 AP 值：
式中 Ps 表示传输变压器原边和副边绕组输出功率之和，Bm 表示磁芯的磁通密度，fs表示驱动信号频率，J 为变压器线圈绕组的电流密度，K 为修正系数，可以表示为：
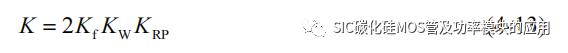
Kf 表示波形系数，和变压器的电压波形相关；系数 KW 表示磁芯的窗口面积的利用率，一般 KW的取值为 0.3 到 0.4；KRP 是表征输出电流是否连续的一个系数，当 KRP为 1 则表示输出电流为连续模式。
根据(4-9)计算出 AP 值，可以确定变压器磁芯的具体规格型号、磁芯材料，查询相关磁芯材料的特性手册，得到磁芯的有效截面积 Ae，来进一步确定变压器次级绕组的匝数：
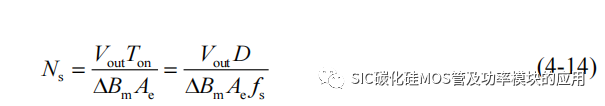
其中 Vout 表示次级绕组输出的驱动电压，ΔBm 表示导通时间内的磁通增量，可以根据磁芯材料确定，最后利用匝数比即可换算出其他绕组匝数。本文所提出的串联型驱动结构，采用 1:1 的匝数比，以有效降低由于关断变压器去磁过程中反向电压的幅值。
4.4 串联驱动器仿真
为了进一步验证提出的变压器隔离型的串联 SiC MOSFET 驱动电路的可行性，本文通过在 PSPICE 软件中搭建了所提出的变压器隔离串联驱动结构驱动单管的仿真模型，搭建的驱动模型中 SiC MOSFET 模型采用 CREE 的 C3M0075120K，一次侧开关 MOSFET 采用 Infineon 的 SPB100N06S2L-05_L1，具有 55V 的耐压，可承受400A 的脉冲电流。
输入驱动信号为 50kHz，占空比为 60%的 PWM，如图 4-5 所示为仿真得到的输出栅源极电压和漏源极电压波形。其中模型中变压器的变比为 1:1，以降低变压器去磁过程中的原边绕组的反向电压。输入电压 20V。
如图 4-4 所示为驱动输出电压的开通关断的瞬间波形结果，其中 40μs 时刻，驱动信号由低电平转为高电平，经过约 20ns 的信号延迟时间，即电感储能充电时间，驱动电压开始上升的，SiC 开始导通；关断的过程也存在接近 20ns 的关断延迟。具体开通关断过程中各器件的电压电流波形如图 4-5 所示。
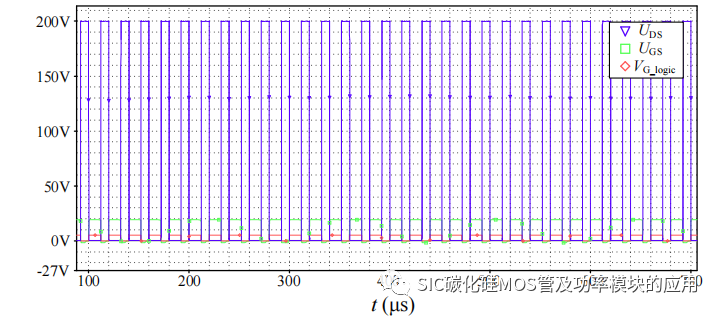图 4-4 驱动电路仿真驱动电压波形
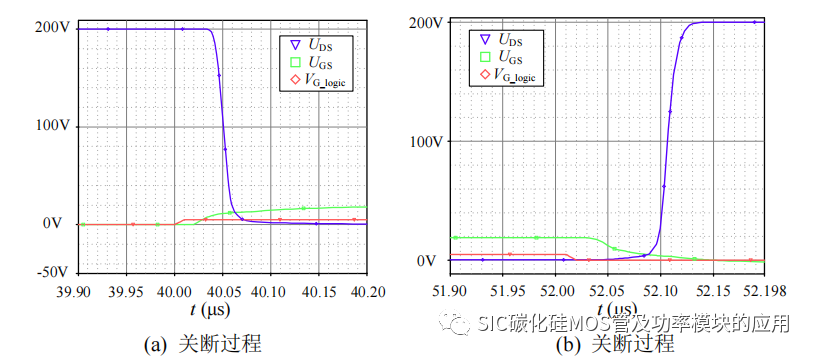图 4-5 开通关断过程驱动电压和漏源极电压仿真结果
具体开通关断过程中各器件的电压电流波形如图 4-6 所示。从图中可以看出，在驱动信号为高时，一次侧开关 MOSFET，S1 导通，变压器初级绕组 N1 承担输入电压，次级绕组 N2 为后级的储能电容 C2 和栅源极电压充电，持续时间较短，之后由于 SiC MOSFET 作为电压型控制器件，主要依靠栅源极电压作为保持开通状态，因此在开通阶段，N2 输出电流基本为 0，与仿真结果中 N2 的输出电流 IL2 的趋势一致，即开通瞬间存在一个较大的充电电流，持续时间较短。在关断过程中，SiC MOSFET的栅源极电容放电，变压器的 N1、N2 绕组同名端电压反向，N1 的等效漏感 L1 和 RCD吸收电容 C1 发生谐振，达到谐振电压后，只要有电阻消耗 N1 中的储能，同时次级绕组 N2 经过电阻去磁，去磁过程会保持栅源极电压在负电压，去磁时间即为关断负压的持续时间，之后当 N1 中存储的能量不足以维持，电压开始下降，直至电压为 0，标志着去磁的结束。而关断负压的电压大小主要由去磁回路等效电阻决定。此外去磁的时间也受到 RCD 参数和驱动频率的限制。当开关频率更高时，需要更小的去磁回路电阻，来保证电去磁时间，防止磁饱和。
为进一步验证串联驱动结构在 SiC MOSFET 串联电路中的效果，搭建了3 个SiC MOSFET 串联的应用电路，变压器的匝数比为 1:1:1:1，SiC MOSFET 的驱动回路参数一致。输入电压降为 15V 以匹配 SiC MOSFET 手册中电压。
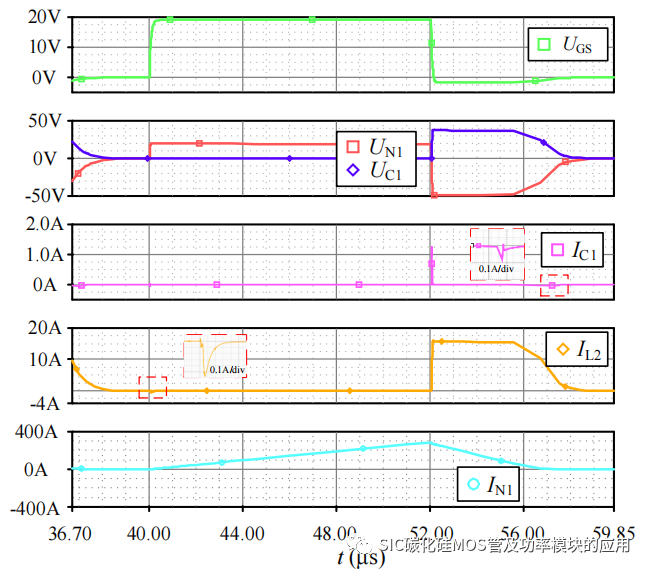图 4-6 驱动电路开关周期内波形
当串联 SiC MOSFET 驱动回路参数完全对称时，仿真结果如图 4-7 所示，此时SiC MOSFET 在关断时各自分担三分之一的母线电压，驱动电压波形重合。进一步验证去磁回路电阻对关断负压的影响，改变去磁回路电阻的大小，得到如图 4-8 所示的串联驱动电压波形。其中 UGS1 到 UGS3 所对应的二次侧绕组回路去磁电阻分别为 2.5Ω、5Ω 和 10Ω。从图 4-8 的仿真结果来看，二次侧的去磁电阻不仅在去磁回路中起到消耗变压器的线圈储能的作用，而且在驱动输出过程中起到限制充电电流的作用，决定栅源极电压的上升时间。在关断后的去磁过程中，由于变压器各个绕组之间耦合必定同时开始进行电感线圈的去磁，由于 SiC MOSFET1 的驱动电阻最小，电感电流瞬间变化更大，根据电感电压关系，UGS1 的对应驱动负电压更大。而且本文所提出基于变压器隔离型的串联驱动电路，依靠变压器的磁场变化对输出绕组所连接的串联 SiCMOSFET 的驱动电压的上升速度进行约束，在动态均压阶段，SiC MOSFET 栅源极电压的同步性得到保证。根据仿真结果 SiC MOSFET 的串联结构中，保证驱动回路参数的一致性是实现 SiC MOSFET 串联均压的前提。
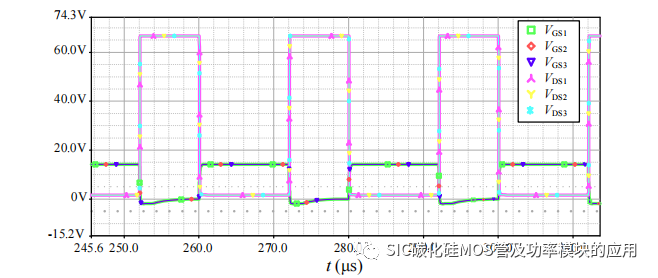图 4-7 驱动回路参数一致下的驱动电压
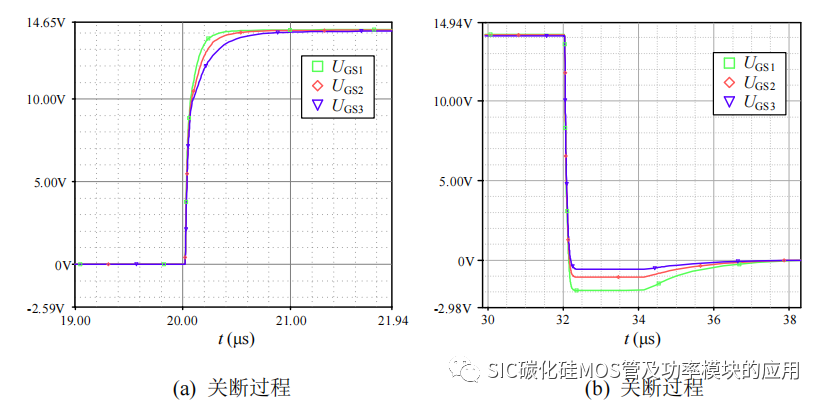图 4-8 去磁电阻不一致下的驱动电压波形
4.5 本章小结
本章针对串联 SiC MOSFET 结构提出一种基于变压器隔离的驱动电路结构，将驱动电平信号转化为功率电压信号，经过变压器传递给串联 SiC MOSFET，可以既保证每一个串联 SiC MOSFET 驱动信号的同步性，同时又可以节省驱动的正负电源，简化了驱动电路的结构。首先对于所提出驱动电路的开关过程和驱动原理进行了分析，并针对 SiC MOSFET 驱动电路给出了相关变压器和 RCD 缓冲电路参数设计，最后结合 PSPICE 仿真软件验证了驱动电路的可行性。
结 论
在中高压大功率场合下，SiC MOSFET 的串并联应用，成为一种高效经济的扩展耐压等级、电流容量的方式，然而较短的开通关断时间，使得寄生参数成为影响SiC MOSFET 并联动态和静态均流效果的主要因素。此外对于串联 SiC 器件，由于驱动源极的电位悬浮，保持驱动信号的一致性成为实现动态均压的重要挑战。因此本文以 SiC MOSFET 作为主要研究对象，针对寄生参数对并联均流的影响和串联驱动电压缺乏一致性的问题展开研究，主要结论如下：
(1) 建立了 SiC MOSFET 的寄生参数模型，分析了 SiC MOSFET 的开通关断过程的波形，建立含有寄生参数变量的电压电流数学模型。结合输出电流函数，量化分析了并联 SiC MOSFET 的动态均流和静态均流过程中寄生参数差异造成并联支路电流存在差异的问题。
(2) 为了验证寄生参数对并联均流效果的影响，搭建了基于并联 SiC MOSFET均流实验平台，对上述寄生参数均流影响进行验证，实验结果证明了动态均流受栅源极电容和驱动电阻影响较大，寄生电感为静态均流主要影响因素，同时也印证了并联动态均流可以依靠并联驱动改善，并联支路对称是一种高效的均流方式。
(3) 基于上述并联均流分析过程得到的相关电压电流函数表达式，分析了开关过程中 SiC MOSFET 器件损耗的主要形式，利用周期离散化的分析思想，给出了损耗、结温和并联均流之间关系，对 SiC MOSFET 自均流特性进行了理论分析验证。在此基础上，结合器件损耗与散热系统之间热平衡关系曲线和 PLECS 仿真结果证明了自均流范围受热平衡条件的约束，只能实现范围内的并联电流自均衡。
(4) 针对目前 SiC MOSFET 串联结构通常采用有源钳位式驱动电路，存在串联SiC MOSFET 的导通延迟、无法实现动态均压的问题，本文提出一种基于多绕组变压器隔离型串联驱动电路方案，其依靠变压器的磁场约束条件，实现串联 SiC MOSFET 的驱动电压同步上升，解决了由于驱动电压不平衡造成的动态均问题。
由于研究深度和时间的限制，本文的研究内容主要针对 SiC MOSFET 的并联均流影响因素和器件特性展开研究，基于上述研究可以继续开展的研究方向有：
(1) 结合本文研究得到的并联均流中主要寄生参数影响规律，可以开展新型并联 SiC MOSFET 结构设计。
(2) 针对本文所提出的串联驱动拓扑，进一步优化结构，提升关断负压的大小和持续时间。
声明：此文来源网络，是出于传递更多信息之目的。若有来源标注错误或侵犯了您的合法权益，请与我们联系，我们将及时更正、删除，谢谢。
厉害